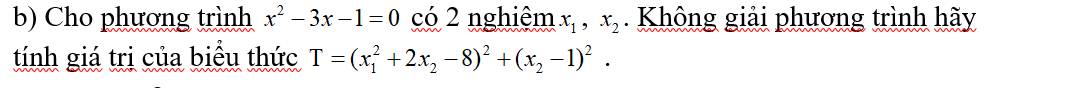Theo định lí Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=3\\x_1x_2=-1\end{matrix}\right.\).
Do \(x_1\) là nghiệm của phương trình nên: \(x_1^2-3x_1-1=0\Leftrightarrow x_1^2=3x_1+1\).
Do đó: \(T=\left(x_1^2+2x_2-8\right)^2+\left(x_2-1\right)^2\)
\(=\left(3x_1+1+2x_2-8\right)^2+\left(x_2-1\right)^2\)
\(=\left[2\left(x_1+x_2\right)+x_1-7\right]^2+\left(x_2-1\right)^2\)
\(=\left(2\cdot3+x_1-7\right)^2+\left(x_2-1\right)^2\)
\(=\left(x_1-1\right)^2+\left(x_2-1\right)^2\)
\(=\left(x_1^2+x_2^2\right)+\left(-2x_1-2x_2\right)+2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2-2\left(x_1+x_2\right)+2\)
\(\Rightarrow T=3^2-2\left(-1\right)-2\cdot3+2=7.\)
Vậy: \(T=7.\)