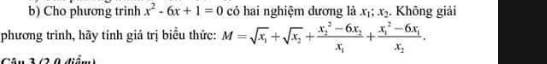Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=6\\x_1x_2=\dfrac{c}{a}=1\end{matrix}\right.\)
\(\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=x_1+x_2+2\sqrt{x_1x_2}=6+2\cdot\sqrt{1}=8\)
=>\(\sqrt{x_1}+\sqrt{x_2}=2\sqrt{2}\)
\(M=\sqrt{x_1}+\sqrt{x_2}+\dfrac{x_2^2-6x_2}{x_1}+\dfrac{x_1^2-6x_1}{x_2}\)
\(=2\sqrt{2}+\dfrac{-1}{x_1}+\dfrac{-1}{x_2}\)
\(=2\sqrt{2}-\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)\)
\(=2\sqrt{2}-\dfrac{x_1+x_2}{x_1x_2}=2\sqrt{2}-\dfrac{6}{1}=2\sqrt{2}-6\)
Đúng 1
Bình luận (0)
