Question

Answer 1

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

=>HB=HC

b: ΔAHB=ΔAHC

=>\(\widehat{BAH}=\widehat{CAH}\)

Xét ΔAMH vuông tại M và ΔANH vuông tại N có

AH chung

\(\widehat{MAH}=\widehat{NAH}\)

Do đó: ΔAMH=ΔANH

=>HM=HN

mà HM<HB(ΔHMB vuông tại M)

nên HN<HB

c: Ta có: DH//AC

=>\(\widehat{DHA}=\widehat{HAC}\)

mà \(\widehat{HAC}=\widehat{HAB}\)

nên \(\widehat{DHA}=\widehat{DAH}\)

=>DA=DH

Ta có: \(\widehat{DAH}+\widehat{DBH}=90^0\)(ΔAHB vuông tại H)

\(\widehat{DHA}+\widehat{DHB}=90^0\)

mà \(\widehat{DAH}=\widehat{DHA}\)

nên \(\widehat{DBH}=\widehat{DHB}\)

=>DB=DH

mà DH=DA

nên DB=DA

=>D là trung điểm của AB

=>\(DH=\dfrac{1}{2}AB\)

Answer 2

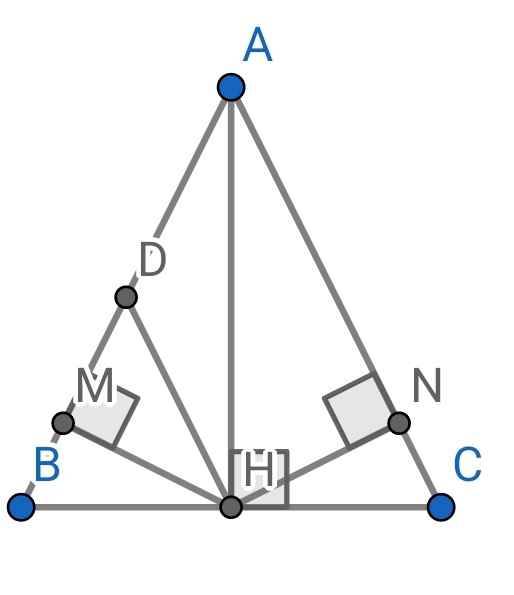
a) Do ∆ABC cân tại A (gt)

AH là đường cao (gt)

⇒ AH cũng là đường trung tuyến

⇒ H là trung điểm của BC

⇒ BH = HC

b) ∆CHN vuông tại N

⇒ CH là cạnh huyền nên là cạnh lớn nhất

⇒ CH > HN

Mà BH = CH (cmt)

⇒ BH > HN

c) ∆ABC cân tại A (gt)

AH là đường cao (gt)

⇒ AH là đường phân giác

⇒ ∠BAH = ∠CAH

⇒ ∠DAH = ∠CAH

Do HD // AC (gt)

⇒ ∠DHA = ∠CAH (so le trong)

Mà ∠DAH = ∠CAH (cmt)

⇒ ∠DHA = ∠DAH

⇒ ∆AHD cân tại D

⇒ DH = AD (1)

Do DH // AC (gt)

⇒ ∠DHB = ∠ACB (đồng vị)

Mà ∠ACB = ∠ABC (∆ABC cân tại A)

⇒ ∠DHB = ∠ABC

⇒ ∠DHB = ∠DBH

⇒ ∆BHD cân tại D

⇒ DH = BD (2)

Từ (1) và (2) ⇒ D là trung điểm của AB

⇒ DH = AD = BD = AB : 2