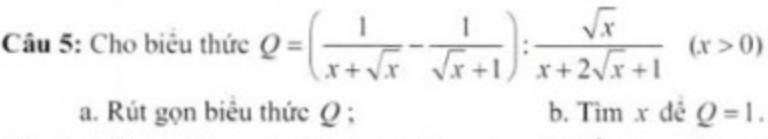Question

Answer 1

a: \(Q=\left(\dfrac{1}{x+\sqrt{x}}-\dfrac{1}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}}{x+2\sqrt{x}+1}\)

\(=\left(\dfrac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}+1}\right)\cdot\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}}\)

\(=\dfrac{1-\sqrt{x}}{\left(\sqrt{x}+1\right)\cdot x}\cdot\left(\sqrt{x}+1\right)^2=\dfrac{\left(1-\sqrt{x}\right)\left(1+\sqrt{x}\right)}{x}=\dfrac{1-x}{x}\)

b: Để Q=1 thì 1-x=x

=>2x=1

=>x=1/2(nhận)