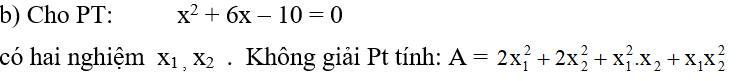Theo Vi-ét ta có: \(\left\{{}\begin{matrix}x_1+x_2=-6\\x_1\cdot x_2=-10\end{matrix}\right.\)
Ta có: \(A=2x_1^2+2x_2^2+x_1^2\cdot x_2+x_1\cdot x_2^2\)
\(=2\left[\left(x_1+x_2\right)^2-2x_1\cdot x_2\right]+x_1x_2\left(x_1+x_2\right)\)
\(=2\left[\left(-6\right)^2-2\cdot\left(-10\right)\right]-10\cdot\left(-6\right)\)
\(=2\left(36+10\right)+60\)
\(=92+60=152\)
Hai bến sông A và B cách nhau 40km. Cùng 1 lúc, 1 chiếc ca nô xuôi dòng từ A dến B và 1 chiếc bè cũng trôi từ A đến B với vận tốc 3km/h. Sau khi đến B, ca nô quay về A ngay và gặp chiếc bè ở 1 địa điểm cách B là 32km. Tính vận tốc ca nô
Cho phương trình
\(x^2-\left(2m-1\right)x-2m-1=0\)
Tìm m để phương trình có 2 nghiệm x1,x2 thỏa mãn \(x_1^3-x_2^3+2\left(x_1^2-x_2^2\right)=0\)
Cho hình vuông ABCD, lấy M thuộc AD. Vẽ \(\left(O;\dfrac{BM}{2}\right)\) cắt AC tại E (E khác A). Gọi K là giao của ME và CD
Chứng mình:
a) Tam giác BME vuông cân
b) EM = ED
c) 4 điểm B, M, D, K thuộc 1 đường tròn
d) BK là tiếp tuyến của (O)
Làm 2 câu cuối hộ mình nha!~
một thựa rông hinh nhật có chu vi 340m . 3 lần chiều dài hơn 4 lần chiều rộng là 40m . tính diên tích
ctiếp tuyến ME và MF (E,F là tiếp điểm) sao cho góc E M O ^ = 30 0 . Biết chu vi ΔMEF là 30 cm
a, Tính độ dài dây EF
b, Tính diện tích ΔMEF
giải các phương trình sau
a) \(\sqrt{\left(2x-1\right)^2}=3\)
b) \(3\sqrt{x}-2\sqrt{9x}+\sqrt{16x}=5\)
c)\(\sqrt{4x+20}-3\sqrt{5+x}+\frac{3}{4}\sqrt{9x+45}=6\)
Lấy C thuộc tia phân giác Oz của góc nhọn xOy. Kẻ CA, CB lần lượt vuông góc Ox, Oy ( A thuộc Ox, B thuộc Oy ) . CM:
a) tam giác AOC = tam giác BOC
b) OC là đường trung trực của AB
c) Kẻ AD vuông góc OB (D thuộc OB). Gọi M là giao điểm của AB với Oz. CM: BM vuông góc OA
Rút gọn các biểu thức sau: 27 a - 3 2 48 v ớ i a > 3
Trong hình 68, đường tròn tâm O có bán kính R = 2cm, góc AOB = 75o.
Tính độ dài hai cung AqB và ApB
Cho hcn(MNPQ) có MQ = 4cm, góc PMG=50 độ a/ Tính MP b/ Kẻ QH ⊥ MP (H ∈ MP). Tính QH, MH c/ Kẻ PK ⊥ QN (K ∈ QN). Gọi O ≡ MN ∩ NQ. C/m: ΔQHO = ΔPKO d/ Tính S(QHKP)
Mk đg cần gấp, giúp mk vs. Cảm ơnnn
