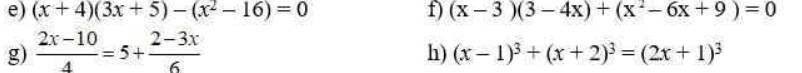e) \(\left(x+4\right)\left(3x+5\right)-\left(x^2-16\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(3x+5\right)-\left(x+4\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(3x+5-x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(2x+9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=-\dfrac{9}{2}\end{matrix}\right.\)
Vậy: ...
f) \(\left(x-3\right)\left(3-4x\right)+\left(x^2-6x+9\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(3-4x\right)+\left(x-3\right)^2=0\)
\(\Leftrightarrow\left(x-3\right)\left(3-4x+x-3\right)=0\)
\(\Leftrightarrow-3x\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
Vậy: ...
g: \(\dfrac{2x-10}{4}=5+\dfrac{2-3x}{6}\)
=>\(\dfrac{3\left(2x-10\right)}{12}=\dfrac{60}{12}+\dfrac{2\left(2-3x\right)}{12}\)
=>3(2x-10)=60+2(2-3x)
=>6x-30=60+4-6x
=>6x-30=64-6x
=>12x=94
=>\(x=\dfrac{94}{12}=\dfrac{47}{6}\)
h: \(\left(x-1\right)^3+\left(x+2\right)^3=\left(2x+1\right)^3\)
=>\(\left(x-1+x+2\right)^3-3\left(x-1+x+2\right)\left(x-1\right)\left(x+2\right)=\left(2x+1\right)^3\)
=>\(\left(2x+1\right)^3-3\left(2x+1\right)\left(x-1\right)\left(x+2\right)=\left(2x+1\right)^3\)
=>\(3\left(2x+1\right)\left(x-1\right)\left(x+2\right)=0\)
=>(2x+1)(x-1)(x+2)=0
=>\(\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\\x=-2\end{matrix}\right.\)