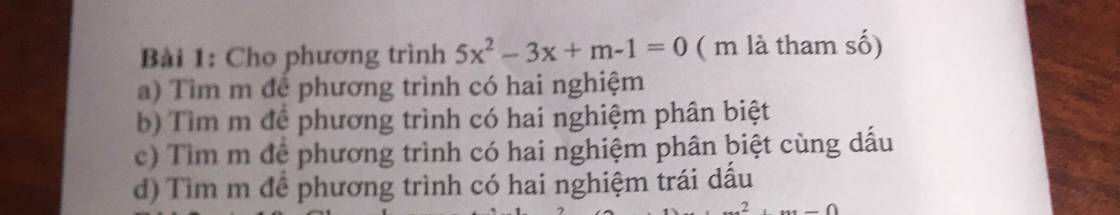a: \(\text{Δ}=\left(-3\right)^2-4\cdot5\cdot\left(m-1\right)=9-20\left(m-1\right)\)
=9-20m+20=-20m+29
Để phương trình có hai nghiệm thì Δ>=0
=>-20m+29>=0
=>-20m>=-29
=>\(m< =\dfrac{29}{20}\)
b: Để phương trình có hai nghiệm phân biệt thì Δ>0
=>-20m+29>0
=>-20m>-29
=>\(m< \dfrac{29}{20}\)
c: Để phương trình có hai nghiệm phân biệt cùng dấu thì
\(\left\{{}\begin{matrix}m< \dfrac{29}{20}\\x_1\cdot x_2>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< \dfrac{29}{20}\\\dfrac{m-1}{5}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{29}{20}\\m-1>0\end{matrix}\right.\)
=>\(1< m< \dfrac{29}{20}\)
d: Để phương trình có hai nghiệm trái dấu thì \(5\left(m-1\right)< 0\)
=>m-1<0
=>m<1