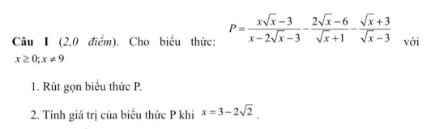1: \(P=\dfrac{x\sqrt{x}-3}{x-2\sqrt{x}-3}-\dfrac{2\sqrt{x}-6}{\sqrt{x}+1}-\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\)
\(=\dfrac{x\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}-\dfrac{2\sqrt{x}-6}{\sqrt{x}+1}-\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\)
\(=\dfrac{x\sqrt{x}-3-\left(2\sqrt{x}-6\right)\left(\sqrt{x}-3\right)-\left(\sqrt{x}+3\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x\sqrt{x}-3-2x+6\sqrt{x}+6\sqrt{x}-18-x-4\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x\sqrt{x}-3x+8\sqrt{x}-24}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}=\dfrac{x+8}{\sqrt{x}+1}\)
2: Thay \(x=3-2\sqrt{2}=\left(\sqrt{2}-1\right)^2\) vào P, ta được:
\(P=\dfrac{3-2\sqrt{2}+8}{\sqrt{\left(\sqrt{2}-1\right)^2}+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}-1+1}\)
\(=\dfrac{11-2\sqrt{2}}{\sqrt{2}}=\dfrac{11\sqrt{2}-4}{2}\)
Lời giải:
1.
\(P=\frac{x\sqrt{x}-3}{(\sqrt{x}+1)(\sqrt{x}-3)}-\frac{(2\sqrt{x}-6)(\sqrt{x}-3)}{(\sqrt{x}+1)(\sqrt{x}-3)}-\frac{(\sqrt{x}+3)(\sqrt{x}+1)}{(\sqrt{x}-3)(\sqrt{x}+1)}\\ =\frac{x\sqrt{x}-3-(2x-12\sqrt{x}+18)-(x+4\sqrt{x}+3)}{(\sqrt{x}+1)(\sqrt{x}-3)}\\ =\frac{x\sqrt{x}-3x+8\sqrt{x}-24}{(\sqrt{x}+1)(\sqrt{x}-3)}\\ =\frac{x(\sqrt{x}-3)+8(\sqrt{x}-3)}{(\sqrt{x}+1)(\sqrt{x}-3)}\\ =\frac{(x+8)(\sqrt{x}-3)}{(\sqrt{x}+1)(\sqrt{x}-3)}=\frac{x+8}{\sqrt{x}+1} \)
2.
Khi $x=3-2\sqrt{2}=(\sqrt{2}-1)^2\Rightarrow \sqrt{x}=\sqrt{2}-1$
\(P=\frac{x+8}{\sqrt{x}+1}=\frac{3-2\sqrt{2}+8}{\sqrt{2}-1+1}=\frac{11-2\sqrt{2}}{\sqrt{2}}\)