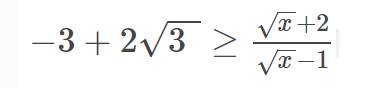ĐKXĐ: x>=0 và x<>1
\(-3+2\sqrt{3}>=\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\)
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}-1}< =2\sqrt{3}-3\)
=>\(\dfrac{\sqrt{x}-1+3}{\sqrt{x}-1}< =2\sqrt{3}-3\)
=>\(1+\dfrac{3}{\sqrt{x}-1}< =2\sqrt{3}-3\)
=>\(\dfrac{3}{\sqrt{x}-1}< =2\sqrt{3}-4\)
=>\(\dfrac{3-\left(2\sqrt{3}-4\right)\left(\sqrt{x}-1\right)}{\sqrt{x}-1}< =0\)
=>\(\dfrac{3-\left(2\sqrt{3}-4\right)\sqrt{x}+\left(2\sqrt{3}-4\right)}{\sqrt{x}-1}< =0\)
=>\(\dfrac{\sqrt{x}\left(4-2\sqrt{3}\right)+2\sqrt{3}-1}{\sqrt{x}-1}< =0\)
mà \(\sqrt{x}\left(4-2\sqrt{3}\right)+2\sqrt{3}-1>0\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x}-1< 0\)
=>\(\sqrt{x}< 1\)
=>0<=x<1
TH1: \(\sqrt{x}-1< 0\Rightarrow\dfrac{\sqrt{x}+2}{\sqrt{x}-1}< 0\)
Mà \(-3+2\sqrt{3}>0\) nên BPT luôn đúng
Vậy \(0\le x< 1\) là nghiệm
TH2: \(\sqrt{x}-1>0\Rightarrow x>1\)
Khi đó BPT tương đương:
\(\left(-3+2\sqrt{3}\right)\left(\sqrt{x}-1\right)\ge\sqrt{x}+2\)
\(\Leftrightarrow\left(-4+2\sqrt{3}\right)\sqrt{x}\ge-1+2\sqrt{3}\)
Vô nghiệm do \(\left\{{}\begin{matrix}-4+2\sqrt{3}< 0\\-1+2\sqrt{3}>0\end{matrix}\right.\)
\(\Rightarrow\left(-4+2\sqrt{3}\right).\sqrt{x}< 0< -1+2\sqrt{3}\)
Vậy nghiệm của BPT là \(0\le x< 1\)