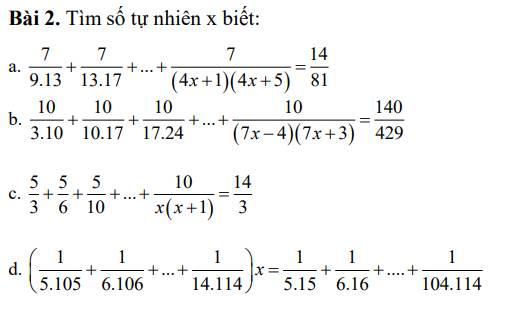a) \(\dfrac{7}{9\cdot13}+\dfrac{7}{13\cdot17}+...+\dfrac{7}{\left(4x+1\right)\left(4x+5\right)}=\dfrac{14}{81}\)
\(\Rightarrow\dfrac{7}{4}\cdot\left[\dfrac{4}{9\cdot13}+\dfrac{4}{13\cdot17}+...+\dfrac{4}{\left(4x+1\right)\left(4x+5\right)}\right]=\dfrac{14}{81}\)
\(\Rightarrow\dfrac{1}{9}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{17}+...+\dfrac{1}{4x+1}-\dfrac{1}{4x+5}=\dfrac{14}{81}:\dfrac{7}{4}\)
\(\Rightarrow\dfrac{1}{9}-\dfrac{1}{4x+5}=\dfrac{8}{81}\)
\(\Rightarrow\dfrac{1}{4x+5}=\dfrac{1}{9}-\dfrac{8}{81}\)
\(\Rightarrow\dfrac{1}{4x+5}=\dfrac{1}{81}\)
\(\Rightarrow4x+5=81\)
\(\Rightarrow4x=81-5\)
\(\Rightarrow4x=76\)
\(\Rightarrow x=\dfrac{76}{4}\)
\(\Rightarrow x=19\)