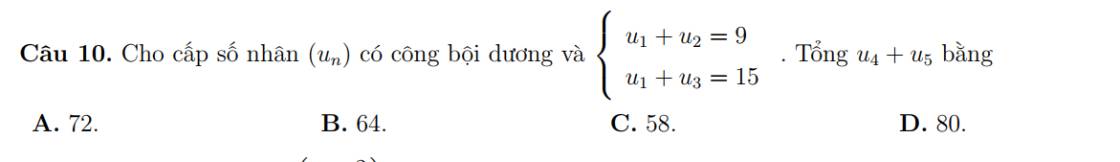\(\left\{{}\begin{matrix}u_1+u_2=9\\u_1+u_3=15\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_1+d=9\\u_1+u_1+2d=15\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2u_1+d=9\\2u_1+2d=15\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1=\dfrac{3}{2}\\d=6\end{matrix}\right.\)
Có: \(u_4=u_1+3d=\dfrac{3}{2}+3.6=\dfrac{39}{2}\)
\(u_5=u_1+4d=\dfrac{3}{2}+4.6=\dfrac{51}{2}\)
\(\Rightarrow u_4+u_5=\dfrac{39}{2}+\dfrac{51}{2}=45\)
\(\Rightarrow\) Không có đáp án chính xác.
Theo đề bài ta có:
\(\left\{{}\begin{matrix}u_1+u_2=9\\u_1+u_3=15\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_1q=9\\u_1+u_1q^2=15\end{matrix}\right.\) `(q>0) `
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{15}{1+q^2}+q\cdot\dfrac{15}{1+q^2}=9\\u_1=\dfrac{15}{1+q^2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{15+15q}{1+q^2}=9\\u_1=\dfrac{15}{1+q^2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15+15q=9+9q^2\\u_1=\dfrac{15}{1+q^2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}9q^2-15q-6=0\Leftrightarrow\left[{}\begin{matrix}q=2\left(tm\right)\\q=-\dfrac{1}{3}\left(ktm\right)\end{matrix}\right.\\u_1=\dfrac{15}{1+4}=3\end{matrix}\right.\)
\(\Rightarrow u_4=3\cdot q^3=3\cdot2^3=24\)
\(\Rightarrow u_5=3\cdot q^4=3\cdot16=48\)
\(u_4+u_5=24+48=72\)
Chọn A