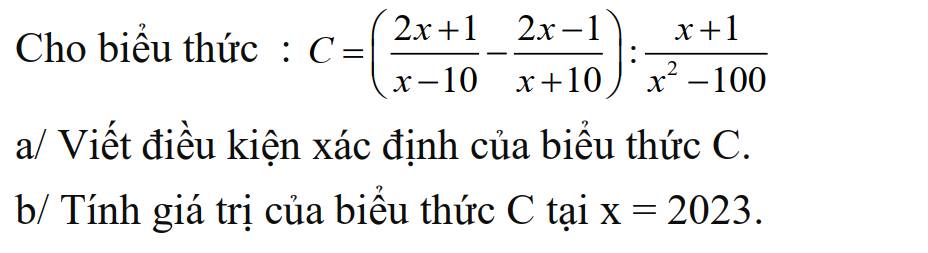a: ĐKXĐ: \(x\notin\left\{10;-10;-1\right\}\)
b: \(C=\left(\dfrac{2x+1}{x-10}-\dfrac{2x-1}{x+10}\right):\dfrac{x+1}{x^2-100}\)
\(=\dfrac{\left(2x+1\right)\left(x+10\right)-\left(2x-1\right)\left(x-10\right)}{\left(x-10\right)\left(x+10\right)}\cdot\dfrac{x^2-100}{x+1}\)
\(=\dfrac{2x^2+20x+x+10-\left(2x^2-20x-x+10\right)}{x+1}\)
\(=\dfrac{2x^2+21x+10-2x^2+21x-10}{x+1}=\dfrac{42x}{x+1}\)
Thay x=2023 vào C, ta được:
\(C=\dfrac{42\cdot2023}{2023+1}=\dfrac{21}{1012}\cdot2023=\dfrac{42483}{1012}\)
a) ĐK: \(\left\{{}\begin{matrix}x-10\ne0\\x+10\ne0\\x^2-100\ne0\\x+1\ne0\end{matrix}\right.\)
\(\Leftrightarrow x\notin\left\{10;-10;-1\right\}\)
b) \(C=\left(\dfrac{2x+1}{x-10}-\dfrac{2x-1}{x+10}\right):\dfrac{x+1}{x^2-100}\)
\(C=\left[\dfrac{\left(2x+1\right)\left(x+10\right)}{\left(x+10\right)\left(x-10\right)}-\dfrac{\left(2x-1\right)\left(x-10\right)}{\left(x+10\right)\left(x-10\right)}\right]:\dfrac{x+1}{\left(x+10\right)\left(x-10\right)}\)
\(C=\dfrac{2x^2+20x+x+10-\left(2x^2-20x-x+10\right)}{\left(x+10\right)\left(x-10\right)}\cdot\dfrac{\left(x+10\right)\left(x-10\right)}{x+1}\)
\(C=\dfrac{2x^2+21x+10-2x^2+21x-10}{x+1}\)
\(C=\dfrac{42x}{x+1}\)
Thay x = 2023 vào C ta có:
\(C=\dfrac{42\cdot2023}{2023+1}=\dfrac{42483}{1012}\)