Bài III:
1: ĐKXĐ: y>=1
\(\left\{{}\begin{matrix}\left|x\right|-\sqrt{y-1}=-1\\\left|x\right|+\dfrac{\sqrt{y-1}}{2}=\dfrac{7}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left|x\right|-\sqrt{y-1}-\left|x\right|-\dfrac{\sqrt{y-1}}{2}=-1-\dfrac{7}{2}=-\dfrac{9}{2}\\\left|x\right|-\sqrt{y-1}=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{y-1}\cdot\dfrac{-3}{2}=-\dfrac{9}{2}\\\left|x\right|-\sqrt{y-1}=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{y-1}=3\\\left|x\right|=-1+\sqrt{y-1}=3-1=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y-1=9\\x\in\left\{2;-2\right\}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=10\left(nhận\right)\\x\in\left\{2;-2\right\}\end{matrix}\right.\)
2: Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{3}{m}\ne\dfrac{-m}{2}\)
=>\(m^2\ne-6\)(luôn đúng)
\(\left\{{}\begin{matrix}3x-my=-9\\mx+2y=16\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=my-9\\mx+2y=16\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=y\cdot\dfrac{m}{3}-3\\m\left(y\cdot\dfrac{m}{3}-3\right)+2y=16\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=y\cdot\dfrac{m}{3}-3\\\dfrac{m^2}{3}\cdot y-3m+2y=16\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=y\cdot\dfrac{m}{3}-3\\y\left(\dfrac{m^2}{3}+2\right)=3m+16\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=y\cdot\dfrac{m}{3}-3\\y=\left(3m+16\right):\dfrac{m^2+6}{3}=\dfrac{3\left(3m+16\right)}{m^2+6}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{3\left(3m+16\right)}{m^2+6}\\x=\dfrac{3\left(3m+16\right)}{m^2+6}\cdot\dfrac{1}{3}-3=\dfrac{3m+16-3m^2-18}{m^2+6}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{3\left(3m+16\right)}{m^2+6}\\x=\dfrac{-3m^2+3m-2}{m^2+6}\end{matrix}\right.\)
x=2y
=>\(\dfrac{-3m^2+3m-2}{m^2+6}=\dfrac{6\left(3m+16\right)}{m^2+6}\)
=>\(-3m^2+3m-2=18m+96\)
=>\(-3m^2-15m-98=0\)
=>\(3m^2+15m+98=0\)
=>\(m\in\varnothing\)
Bài II:
Gọi số sản phẩm đơn vị thứ nhất sản xuất được trong tháng thứ nhất là x(sản phẩm)
(ĐK: \(x\in Z^{^+}\))
Số sản phẩm đơn vị thứ hai sản xuất được trong tháng thứ nhất là: 1800-x(sản phẩm)
Số sản phẩm đơn vị thứ nhất sản xuất được trong tháng thứ hai là x(1+20%)=1,2x(sản phẩm)
Số sản phẩm đơn vị thứ hai sản xuất được trong tháng thứ hai là: (1-15%)*(1800-x)
=0,85(1800-x)(sản phẩm)
Theo đề, ta có phương trình:
\(1,2x+0,85\left(1800-x\right)=1800+24\)
=>\(0,35x+1530=1824\)
=>0,35x=294
=>x=294:0,35=840(nhận)
Vậy: Số sản phẩm đơn vị thứ nhất sản xuất được trong tháng đầu tiên là 840 sản phẩm
Số sản phẩm đơn vị thứ hai sản xuất được trong tháng thứ hai là 1800-840=960 sản phẩm
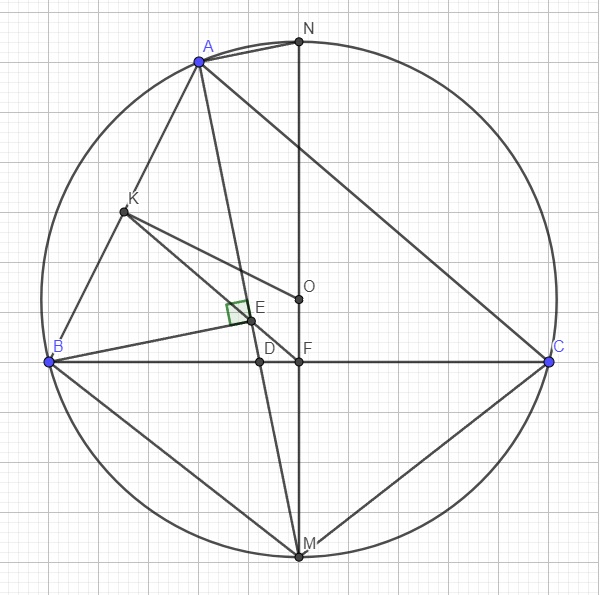
4.
a.
Xét hai tam giác ABD và AMC có:
\(\left\{{}\begin{matrix}\widehat{BAD}=\widehat{MAC}\left(\text{AM là phân giác}\right)\\\widehat{ABD}=\widehat{AMC}\left(\text{cùng chắn AC}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABD\sim\Delta AMC\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AD}{AC}\Rightarrow AB.AC=AD.AM\)
b.
Do \(\widehat{BAM}=\widehat{CAM}\Rightarrow BM=CM\)
Đồng thời \(OB=OC=R\Rightarrow OM\) hay MN là trung trực của BC
\(\Rightarrow MN\perp BC\) tại F và F là trung điểm BC
\(\Rightarrow\) E và F cùng nhìn BM dưới 1 góc vuông nên BEFM nội tiếp
c.
Do BEFM nội tiếp \(\Rightarrow\widehat{BME}=\widehat{BFE}\) (cùng chắn BE)
Mà \(\widehat{BME}=\widehat{BAC}\) (cùng chắn cung AB của (O))
\(\Rightarrow\widehat{BFE}=\widehat{BAC}\)
\(\Rightarrow FK||AC\) (hai góc đồng vị bằng nhau)
Mà F là trung điểm BC nên FK là đường trung bình tam giác ABC
\(\Rightarrow K\) là trung điểm AB
Do K là trung điểm AB \(\Rightarrow OK\perp AB\) tại K
Áp dụng định lý Pitago:
\(R^2=OB^2=BK^2+OK^2\ge\dfrac{1}{2}\left(BK+OK\right)^2\)
\(\Rightarrow BK+OK\le R\sqrt{2}\)
Dấu "=" xảy ra khi và chỉ khi \(BK=OK\Rightarrow\Delta AOB\) vuông cân tại O
Hay A là điểm trên cung AB sao cho \(\widehat{AOB}=90^0\) thì \(BK+OK\) lớn nhất
5.
\(\left(4x-1\right)\sqrt{x^2+1}=2x^2+2x+1\)
\(\Leftrightarrow2\left(x^2+1\right)-\left(4x-1\right)\sqrt{x^2+1}+2x-1=0\)
Đặt \(\sqrt{x^2+1}=t>0\)
\(\Rightarrow2t^2-\left(4x-1\right)t+2x-1=0\)
\(\Leftrightarrow2t^2+t-1-2x\left(2t-1\right)=0\)
\(\Leftrightarrow\left(t+1\right)\left(2t-1\right)-2x\left(2t-1\right)=0\)
\(\Leftrightarrow\left(2t-1\right)\left(t-2x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2t=1\\t=2x-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2\sqrt{x^2+1}=1\\\sqrt{x^2+1}=2x-1\left(x\ge\dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4\left(x^2+1\right)=1\\x^2+1=4x^2-4x+1\left(x\ge\dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=-\dfrac{3}{4}\left(vn\right)\\3x^2-4x=0\left(x\ge\dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0< \dfrac{1}{2}\left(loại\right)\\x=\dfrac{4}{3}\end{matrix}\right.\)