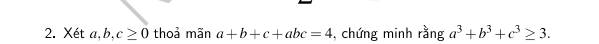Chúng ta có điều kiện \(a+b+c+abc=4\). Để chứng minh \(a^3+b^3+c^3 \geq 3\), sử dụng bất đẳng thức AM-GM:
\[a^3+b^3+c^3 \geq 3\sqrt[3]{a^3b^3c^3}.\]
Giả sử \(abc = x^3\), thì bất đẳng thức trở thành:
\[a^3+b^3+c^3 \geq 3x.\]
Chúng ta cần chứng minh \(x \geq 1\). Áp dụng bất đẳng thức AM-GM cho điều kiện \(a+b+c+abc=4\), ta có:
\[4 = a+b+c+abc \geq 4\sqrt[4]{a \cdot b \cdot c \cdot abc} = 4\sqrt[4]{x^4} = 4x.\]
Từ đó, ta suy ra \(x \leq 1\). Do đó, \(x = abc \leq 1\).
Bây giờ, áp dụng AM-GM cho \(a^3+b^3+c^3\), ta có:
\[a^3+b^3+c^3 \geq 3\sqrt[3]{a^3b^3c^3}.\]
Với \(abc \leq 1\), ta có \(\sqrt[3]{a^3b^3c^3} \leq 1\), và từ đó suy ra \(a^3+b^3+c^3 \geq 3\), hoàn thành chứng minh.
Áp dụng bất đẳng thức Cauchy, ta có:
\(\left\{{}\begin{matrix}a^3+1+1\ge3a\\b^3+1+1\ge3b\\c^3+1+1\ge3c\\a^3+b^3+c^3\ge3abc\end{matrix}\right.\)
\(\Rightarrow2\left(a^3+b^3+c^3\right)\ge3\left(a+b+c+abc\right)-6=3.4-6=6\)
\(\Rightarrow a^3+b^3+c^3\ge3\left(đpcm\right)\)
Đẳng thức xảy ra khi a=b=c=1