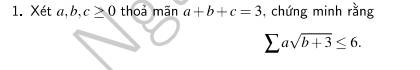Để chứng minh bất đẳng thức đã cho, ta sử dụng bất đẳng thức Cauchy-Schwarz:
\[
\left( \sum a \sqrt{b+3} \right)^2 \leq \left( \sum a^2 \right) \left( \sum (b+3) \right).
\]
Ta cần chứng minh rằng \(\left( \sum a^2 \right) \left( \sum (b+3) \right) \leq 36\).
Từ điều kiện \(a+b+c=3\), ta có \(a^2+b^2+c^2+2(ab+bc+ca)=9\). Do đó, \(\sum a^2 = 9 - 2(ab+bc+ca)\).
Thay vào bất đẳng thức cần chứng minh, ta có:
\[
\left( 9 - 2(ab+bc+ca) \right) \left( 3(ab+bc+ca+9) \right) \leq 36.
\]
Mở rộng và rút gọn bất đẳng thức trên, ta được:
\[
(ab+bc+ca)^2 - 6(ab+bc+ca) + 27 \geq 0.
\]
Đặt \(x = ab+bc+ca\), ta có:
\[
x^2 - 6x + 27 \geq 0.
\]
Để chứng minh điều này, ta sẽ chứng minh rằng \(\Delta \leq 0\), với \(\Delta\) là biểu thức dưới dấu căn bậc hai trong công thức tính nghiệm của phương trình bậc hai.
\(\Delta = (-6)^2 - 4(1)(27) = 36 - 108 = -72 < 0\).
Vì \(\Delta < 0\), nên ta có \(x^2 - 6x + 27 \geq 0\).
Do đó, ta kết luận rằng \(\sum a \sqrt{b+3} \leq 6\).