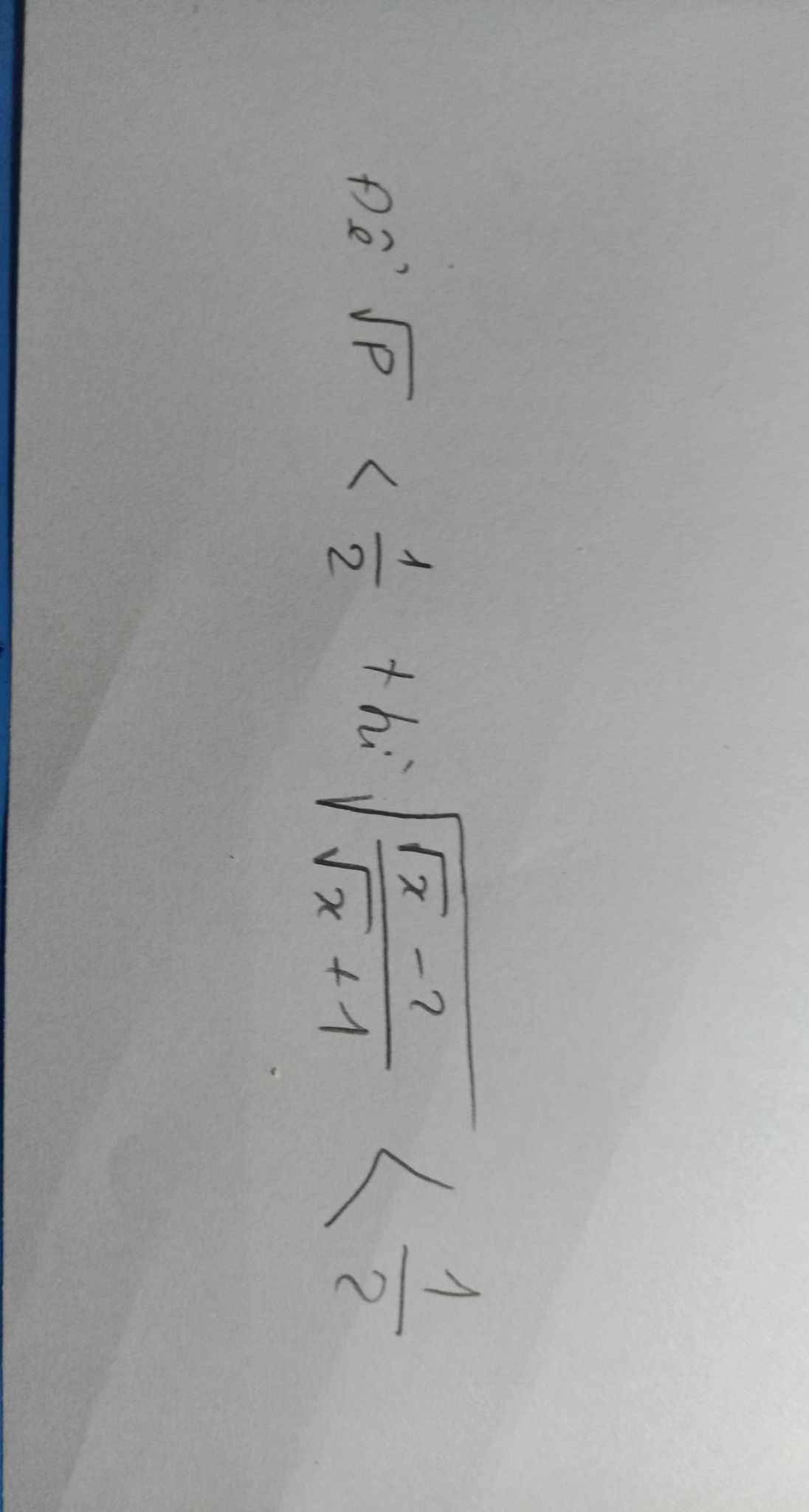ĐKXĐ: x>=0
\(\sqrt{\dfrac{\sqrt{x}-2}{\sqrt{x}+1}}< \dfrac{1}{2}\)
=>\(\left\{{}\begin{matrix}\dfrac{\sqrt{x}-2}{\sqrt{x}+1}>=0\\\dfrac{\sqrt{x}-2}{\sqrt{x}+1}< \dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}-2>=0\\\dfrac{\sqrt{x}-2}{\sqrt{x}+1}-\dfrac{1}{4}< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}>=2\\\dfrac{4\left(\sqrt{x}-2\right)-\sqrt{x}-1}{4\left(\sqrt{x}+1\right)}< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=4\\4\sqrt{x}-8-\sqrt{x}-1< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=4\\3\sqrt{x}< 9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=4\\\sqrt{x}< 3\end{matrix}\right.\Leftrightarrow4< =x< 9\)