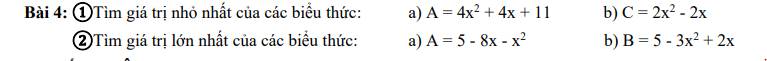1:
a: \(A=4x^2+4x+11\)
\(=4x^2+4x+1+10\)
\(=\left(4x^2+4x+1\right)+10\)
\(=\left(2x+1\right)^2+10>=10\forall x\)
Dấu '=' xảy ra khi 2x+1=0
=>2x=-1
=>\(x=-\dfrac{1}{2}\)
b: \(C=2x^2-2x\)
\(=2\left(x^2-x\right)\)
\(=2\left(x^2-x+\dfrac{1}{4}-\dfrac{1}{4}\right)\)
\(=2\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{2}>=-\dfrac{1}{2}\)
Dấu '=' xảy ra khi x-1/2=0
=>x=1/2
2:
a: \(A=-x^2-8x+5\)
\(=-x^2-8x-16+21\)
\(=-\left(x^2+8x+16\right)+21\)
\(=-\left(x+4\right)^2+21< =21\forall x\)
Dấu '=' xảy ra khi x+4=0
=>x=-4
b: \(B=-3x^2+2x+5\)
\(=-3\left(x^2-\dfrac{2}{3}x-\dfrac{5}{3}\right)\)
\(=-3\left(x^2-2\cdot x\cdot\dfrac{1}{3}+\dfrac{1}{9}-\dfrac{16}{9}\right)\)
\(=-3\left(x-\dfrac{1}{3}\right)^2+\dfrac{16}{3}< =\dfrac{16}{3}\forall x\)
Dấu '=' xảy ra khi x-1/3=0
=>x=1/3
1)
a) \(A=4x^2+4x+11\)
\(=\left(4x^2+4x+1\right)+10\)
\(=\left[\left(2x\right)^2+2\cdot2x\cdot1+1^2\right]+10\)
\(=\left(2x+1\right)^2+10\)
Ta thấy: \(\left(2x+1\right)^2\ge0\forall x\)
\(\Rightarrow A=\left(2x+1\right)^2+10\ge10\forall x\)
Dấu \("="\) xảy ra khi: \(2x+1=0\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(Min_A=10\) khi \(x=-\dfrac{1}{2}\).
b) \(C=2x^2-2x\)
\(=2\left(x^2-x\right)\)
\(=2\left(x^2-x+\dfrac{1}{4}\right)-2\cdot\dfrac{1}{4}\)
\(=2\left[x^2-2\cdot x\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2\right]-\dfrac{1}{2}\)
\(=2\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{2}\)
Ta thấy: \(\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow C=2\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{2}\ge-\dfrac{1}{2}\forall x\)
Dấu \("="\) xảy ra khi: \(x-\dfrac{1}{2}=0\Leftrightarrow x=\dfrac{1}{2}\)
Vậy \(Min_C=-\dfrac{1}{2}\) khi \(x=\dfrac{1}{2}\).
2)
a) \(A=5-8x-x^2\)
\(=-\left(x^2+8x\right)+5\)
\(=-\left(x^2+8x+16\right)+16+5\)
\(=-\left(x^2+2\cdot x\cdot4+4^2\right)+21\)
\(=-\left(x+4\right)^2+21\)
Ta thấy: \(\left(x+4\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x+4\right)^2\le0\forall x\)
\(\Rightarrow A=-\left(x+4\right)^2+21\le21\forall x\)
Dấu \("="\) xảy ra khi: \(x+4=0\Leftrightarrow x=-4\)
Vậy \(Max_A=21\) khi \(x=-4\).
b) \(B=5-3x^2+2x\)
\(=-\left(3x^2-2x\right)+5\)
\(=-3\left(x^2-\dfrac{2}{3}x\right)+5\)
\(=-3\left(x^2-\dfrac{2}{3}x+\dfrac{1}{9}\right)+3\cdot\dfrac{1}{9}+5\)
\(=-3\left[x^2-2\cdot x\cdot\dfrac{1}{3}+\left(\dfrac{1}{3}\right)^2\right]+\dfrac{1}{3}+5\)
\(=-3\left(x-\dfrac{1}{3}\right)^2+\dfrac{16}{3}\)
Ta thấy: \(\left(x-\dfrac{1}{3}\right)^2\ge0\forall x\)
\(\Rightarrow-3\left(x-\dfrac{1}{3}\right)^2\le0\forall x\)
\(\Rightarrow B=-3\left(x-\dfrac{1}{3}\right)^2+\dfrac{16}{3}\le\dfrac{16}{3}\forall x\)
Dấu \("="\) xảy ra khi: \(x-\dfrac{1}{3}=0\Leftrightarrow x=\dfrac{1}{3}\)
Vậy \(Max_B=\dfrac{16}{3}\) khi \(x=\dfrac{1}{3}\).
\(\text{#}Toru\)