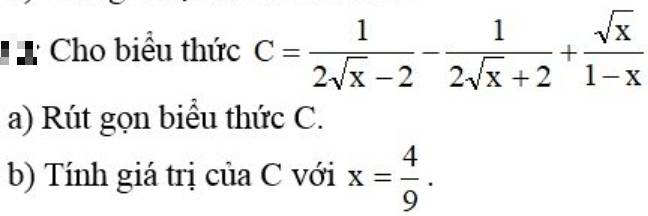Question

Answer 1

a) \(C=\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}+\dfrac{\sqrt{x}}{1-x}\left(x\ge0;x\ne1\right)\)

\(C=\dfrac{1}{2\left(\sqrt{x}-1\right)}-\dfrac{1}{2\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}}{x-1}\)

\(C=\dfrac{\sqrt{x}+1}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}-1}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{2\sqrt{x}}{2\left(\sqrt{x}+1\right)\left(\sqrt{x-1}\right)}\)

\(C=\dfrac{\sqrt{x}+1-\sqrt{x}+1-2\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(C=\dfrac{-2\sqrt{x}+2}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(C=\dfrac{-2\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(C=\dfrac{-1}{\sqrt{x}+1}\) 

b) Thay \(x=\dfrac{4}{9}\) vào C ta có:

\(C=\dfrac{-1}{\sqrt{\dfrac{4}{9}}+1}=\dfrac{-1}{\dfrac{2}{3}+1}=\dfrac{-1}{\dfrac{5}{3}}=-\dfrac{3}{5}\)