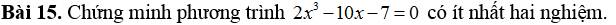Đặt \(f\left(x\right)=2x^3-10x-7\)
\(f\left(-2\right)=2\cdot\left(-2\right)^3-10\cdot\left(-2\right)-7=-3\)
\(f\left(-1\right)=2\cdot\left(-1\right)^3-10\cdot\left(-1\right)-7=2-7+10=5\)
\(f\left(0\right)=2\cdot0^3-10\cdot0-7=-7\)
Vì \(f\left(-2\right)\cdot f\left(-1\right)< 0\) nên phương trình \(2x^3-10x-7=0\) sẽ có ít nhất 1 nghiệm nằm trong khoảng (-2;-1)
Vì \(f\left(-1\right)\cdot f\left(0\right)=-35< 0\)
nên phương trình \(2x^3-10x-7=0\) sẽ có ít nhất 1 nghiệm nằm trong khoảng (-1;0)
Do đó: Phương trình \(2x^3-10x-7=0\) sẽ có ít nhất 2 nghiệm
Đúng 0
Bình luận (1)
