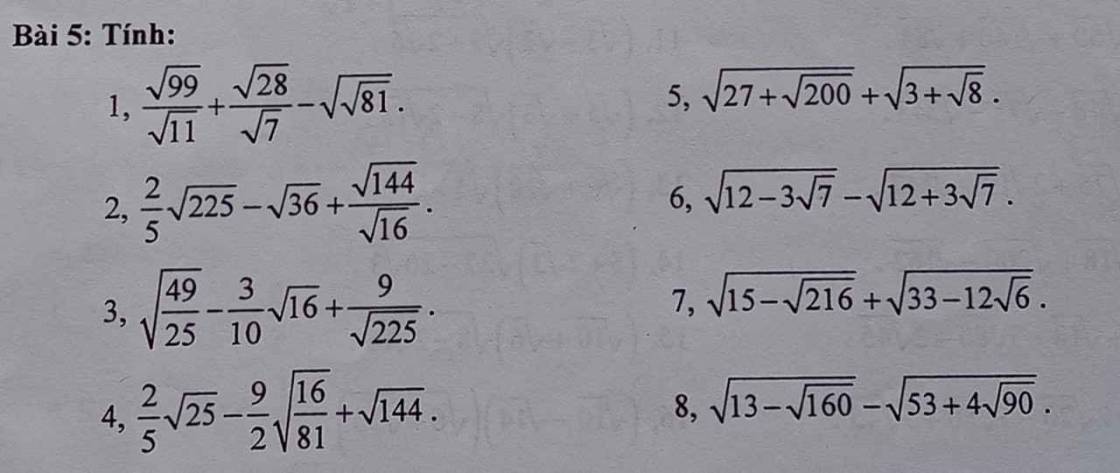1) \(\dfrac{\sqrt{99}}{\sqrt{11}}+\dfrac{\sqrt{28}}{\sqrt{7}}-\sqrt{\sqrt{81}}\)
\(=\sqrt{\dfrac{99}{11}}+\sqrt{\dfrac{28}{7}}-\sqrt{9}\)
\(=\sqrt{9}+\sqrt{4}-\sqrt{9}\)
\(=3+2-3\)
\(=2\)
2) \(\dfrac{2}{5}\sqrt{225}-\sqrt{36}+\dfrac{\sqrt{144}}{\sqrt{16}}\)
\(=\dfrac{2}{5}\cdot15-6+\dfrac{12}{4}\)
\(=2\cdot3-6+3\)
\(=6-6+3\)
\(=3\)
3) \(\sqrt{\dfrac{49}{25}}-\dfrac{3}{10}\sqrt{16}+\dfrac{9}{\sqrt{225}}\)
\(=\dfrac{\sqrt{49}}{\sqrt{25}}-\dfrac{3\cdot4}{10}+\dfrac{9}{15}\)
\(=\dfrac{7}{5}-\dfrac{6}{5}+\dfrac{3}{5}\)
\(=\dfrac{4}{5}\)
4) \(\dfrac{2}{5}\sqrt{25}-\dfrac{9}{2}\sqrt{\dfrac{16}{81}}+\sqrt{144}\)
\(=\dfrac{2}{5}\cdot5-\dfrac{9}{2}\cdot\dfrac{\sqrt{16}}{\sqrt{81}}+12\)
\(=2-\dfrac{9}{2}\cdot\dfrac{4}{9}+12\)
\(=2-2+12\)
\(=12\)