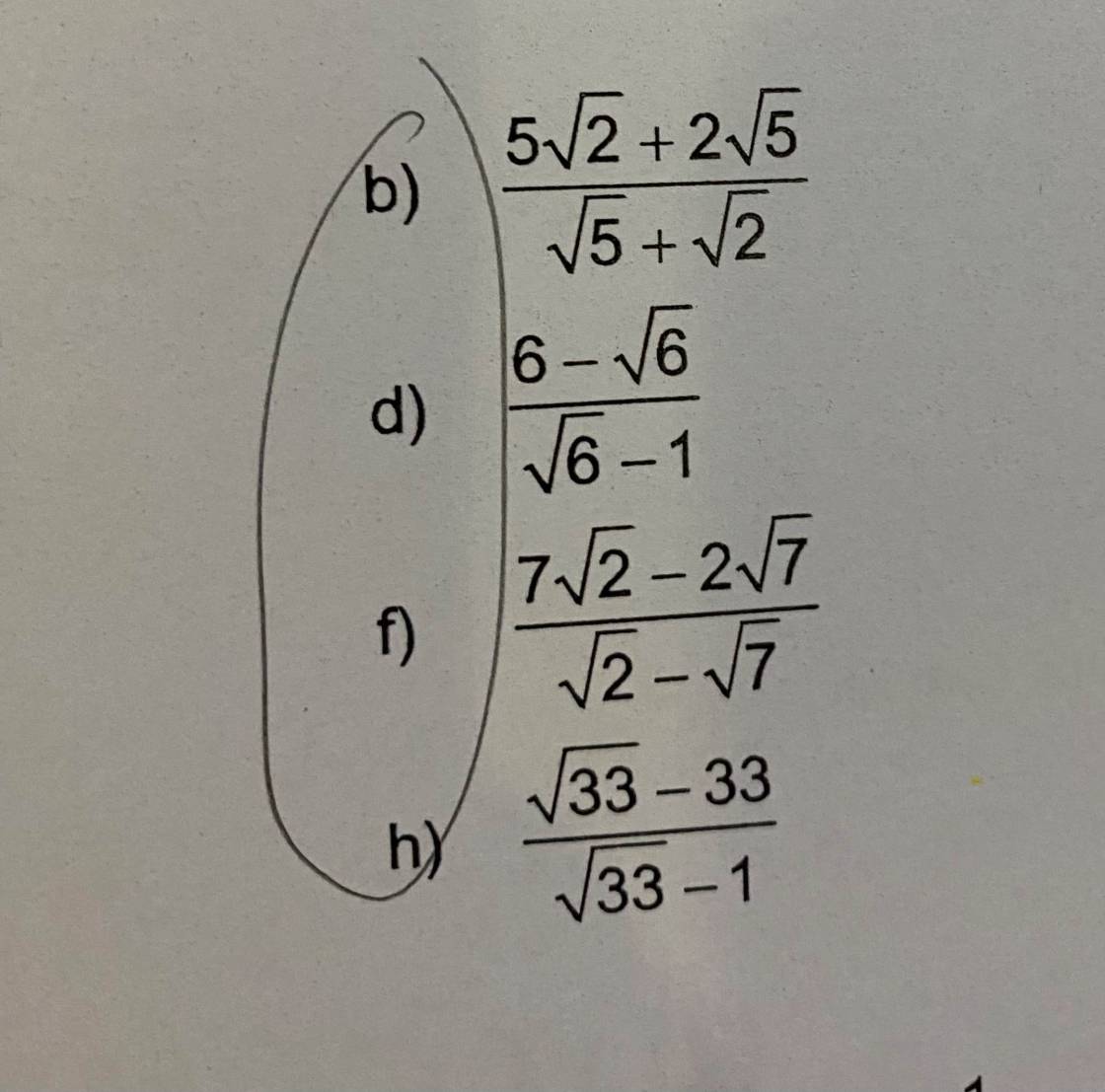b: \(=\dfrac{\sqrt{10}\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{5}+\sqrt{2}}=\sqrt{10}\)
d: \(=\dfrac{\sqrt{6}\cdot\sqrt{6}-\sqrt{6}\cdot1}{\sqrt{6}-1}\)
\(=\dfrac{\sqrt{6}\left(\sqrt{6}-1\right)}{\sqrt{6}-1}=\sqrt{6}\)
f: \(=\dfrac{\sqrt{14}\cdot\sqrt{7}-\sqrt{14}\cdot\sqrt{2}}{-\left(\sqrt{7}-\sqrt{2}\right)}\)
\(=\dfrac{-\sqrt{14}\left(\sqrt{7}-\sqrt{2}\right)}{\sqrt{7}-\sqrt{2}}=-\sqrt{14}\)
h: \(=\dfrac{\sqrt{33}\left(1-\sqrt{33}\right)}{-\left(1-\sqrt{33}\right)}=-\sqrt{33}\)
\(b)=\dfrac{\left(5\sqrt{2}+2\sqrt{5}\right)\left(\sqrt{5}-\sqrt{2}\right)}{5-2}\\ =\dfrac{5\sqrt{10}-10+10-2\sqrt{10}}{3} \\ =\dfrac{3\sqrt{10}}{3}=\sqrt{10}\\ d)=\dfrac{\left(6-\sqrt{6}\right)\left(\sqrt{6}+1\right)}{6-1}\\ =\dfrac{6\sqrt{6}+6-6-\sqrt{6}}{5}\\ =\dfrac{5\sqrt{6}}{5}=\sqrt{6}\)
\(f)=\dfrac{\left(7\sqrt{2}-2\sqrt{7}\right)\left(\sqrt{2}+\sqrt{7}\right)}{2-7}\\ =\dfrac{14+7\sqrt{14}-2\sqrt{14}-14}{-5}\\ =\dfrac{5\sqrt{14}}{-5}\\ =-\sqrt{14}\)
\(h)=\dfrac{\left(\sqrt{33}-33\right)\left(\sqrt{33}+1\right)}{33-1}\\ =\dfrac{33+\sqrt{33}-33\sqrt{33}-33}{32}\\ =\dfrac{-32\sqrt{33}}{32}\\ =-\sqrt{33}\)