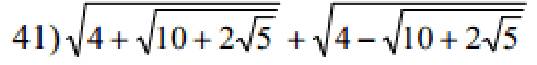\(\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10-2\sqrt{5}}}\)
\(=\sqrt{\left(4+\sqrt{10+2\sqrt{5}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\right)^2}\)
\(=\sqrt{4+\sqrt{10+2\sqrt{5}}+4-\sqrt{10+2\sqrt{5}}+2\sqrt{\left(4+\sqrt{10+2\sqrt{5}}\right)\left(4-\sqrt{10+2\sqrt{5}}\right)}}\)
\(=\sqrt{8+2\sqrt{4^2-\left(\sqrt{10+2\sqrt{5}}\right)^2}}\)
\(=\sqrt{8+2\sqrt{16-10-2\sqrt{5}}}\)
\(=\sqrt{8+2\sqrt{6-2\sqrt{5}}}\)
\(=\sqrt{8+2\sqrt{\left(\sqrt{5}\right)^2-2\sqrt{5}\cdot1+1^2}}\)
\(=\sqrt{8+2\sqrt{\left(\sqrt{5}-1\right)^2}}\)
\(=\sqrt{8+2\left|\sqrt{5}-1\right|}\)
\(=\sqrt{8+2\sqrt{5}-2}\)
\(=\sqrt{6+2\sqrt{5}}\)
\(=\sqrt{\left(\sqrt{5}\right)^2+2\sqrt{5}\cdot1+1^2}\)
\(=\sqrt{\left(\sqrt{5}+1\right)^2}\)
\(=\sqrt{5}+1\)