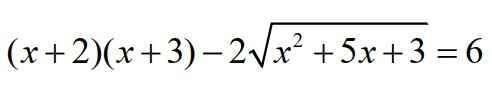`(x+2)(x+3)-2 \sqrt{x^2+5x+3}=6(x >=-1` hoăc `x<=-3/2)`
`<=> ( x^2+5x+6)-2 \sqrt{x^2+5x+3}=6`
Đặt `x^2+5x+3=t(t>=0)`
`<=> t+3-2 \sqrt{t}-6=0`
`<=> t-2\sqrt{t}-3=0`
`<=> ( \sqrt{t}-3)(\sqrt{t}+1)=0`
Do `t>=0=> \sqrt{t}+1>0`
`=> \sqrt{t}-3=0`
`<=> \sqrt{t}=3`
`<=>t=9`
Với `t=9<=>x^2+5x+3=9`
`<=> x^2+5x-6=0`
`<=>(x-1)(x+6)=0`
`<=> [(x-1=0),(x+6=0):}`
`<=> [(x=1(tm)),(x=-6(tm)):}`
Vậy phương trình có tập nghiệm `S={1;-6}`
Đúng 3
Bình luận (0)
