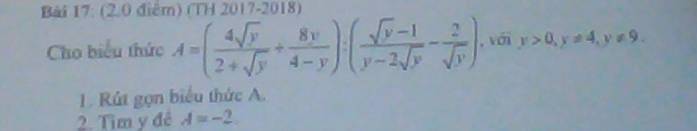\(1,A=\left(\dfrac{4\sqrt{y}}{2+\sqrt{y}}+\dfrac{8y}{4-y}\right):\left(\dfrac{\sqrt{y}-1}{y-2\sqrt{y}}-\dfrac{2}{\sqrt{y}}\right)\left(dk:y>0,y\ne4,y\ne9\right)\\ =\left(\dfrac{4\sqrt{y}}{\sqrt{y}+2}-\dfrac{8y}{\left(\sqrt{y}-2\right)\left(\sqrt{y}+2\right)}\right):\left(\dfrac{\sqrt{y}-1}{\sqrt{y}\left(\sqrt{y}-2\right)}-\dfrac{2}{\sqrt{y}}\right)\)
\(=\dfrac{4\sqrt{y}\left(\sqrt{y}-2\right)-8y}{\left(\sqrt{y}-2\right)\left(\sqrt{y}+2\right)}.\dfrac{\sqrt{y}\left(\sqrt{y}-2\right)}{\sqrt{y}-1-2\left(\sqrt{y}-2\right)}\\ =\dfrac{4y-8\sqrt{y}-8y}{\sqrt{y}+2}.\dfrac{\sqrt{y}}{\sqrt{y}-1-2\sqrt{y}+4}\\ =\dfrac{-4y-8\sqrt{y}}{\sqrt{y}+2}.\dfrac{\sqrt{y}}{-\sqrt{y}+3}\\ =\dfrac{-4\sqrt{y}\left(\sqrt{y}+2\right).\sqrt{y}}{\left(\sqrt{y}+2\right)\left(3-\sqrt{y}\right)}\\ =\dfrac{-4y}{3-\sqrt{y}}\)
\(2,A=-2\Leftrightarrow\dfrac{-4y}{3-\sqrt{y}}=-2 \Leftrightarrow\dfrac{-4y+2\left(3-\sqrt{y}\right)}{3-\sqrt{y}}=0\\ \Leftrightarrow-4y+6-2\sqrt{y}=0\\ \Leftrightarrow x=1\left(tm\right)\)
Vậy \(x=1\) thì \(A=-2\).
1) \(A=\left(\dfrac{4\sqrt{y}}{2+\sqrt{y}}+\dfrac{8y}{4-y}\right):\left(\dfrac{\sqrt{y}-1}{y-2\sqrt{y}}-\dfrac{2}{\sqrt{y}}\right)\)
\(A=\left(\dfrac{4\sqrt{y}}{\sqrt{y}+2}-\dfrac{8y}{y-4}\right):\left[\dfrac{\sqrt{y}-1}{\sqrt{y}\left(\sqrt{y}-2\right)}-\dfrac{2}{\sqrt{y}}\right]\)
\(A=\left[\dfrac{4\sqrt{y}\left(\sqrt{y}-2\right)}{\left(\sqrt{y}+2\right)\left(\sqrt{y}-2\right)}-\dfrac{8y}{\left(\sqrt{y}+2\right)\left(\sqrt{y}-2\right)}\right]:\left[\dfrac{\sqrt{y}-1}{\sqrt{y}\left(\sqrt{y}-2\right)}-\dfrac{2\left(\sqrt{y}-2\right)}{\sqrt{y}\left(\sqrt{y}-2\right)}\right]\)
\(A=\dfrac{4y-8\sqrt{y}-8y}{\left(\sqrt{y}+2\right)\left(\sqrt{y}-2\right)}:\dfrac{\sqrt{y}-1-2\sqrt{y}+4}{\sqrt{y}\left(\sqrt{y}-2\right)}\)
\(A=\dfrac{-4y-8\sqrt{y}}{\left(\sqrt{y}-2\right)\left(\sqrt{y}+2\right)}\cdot\dfrac{\sqrt{y}\left(\sqrt{y}-2\right)}{-\sqrt{y}+3}\)
\(A=\dfrac{-4\sqrt{y}\left(\sqrt{y}+2\right)}{\left(\sqrt{y}-2\right)\left(\sqrt{y}+2\right)}\cdot\dfrac{\sqrt{y}\left(\sqrt{y}-2\right)}{-\left(\sqrt{y}-3\right)}\)
\(A=\dfrac{-4y}{-\sqrt{y}+3}\)
\(A=\dfrac{-4y}{-\left(\sqrt{y}-3\right)}=\dfrac{4y}{\sqrt{y}-3}\)
2) \(A=-2\) khi:
\(\dfrac{4y}{\sqrt{y}-3}=-2\)
\(\Leftrightarrow4y=-2\sqrt{y}+6\)
\(\Leftrightarrow4y+2\sqrt{y}-6=0\)
\(\Leftrightarrow2\left(\sqrt{x}-1\right)\left(2\sqrt{x}+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\2\sqrt{x}=-3\left(sai\right)\end{matrix}\right.\)
\(\Leftrightarrow x=1\left(tm\right)\)