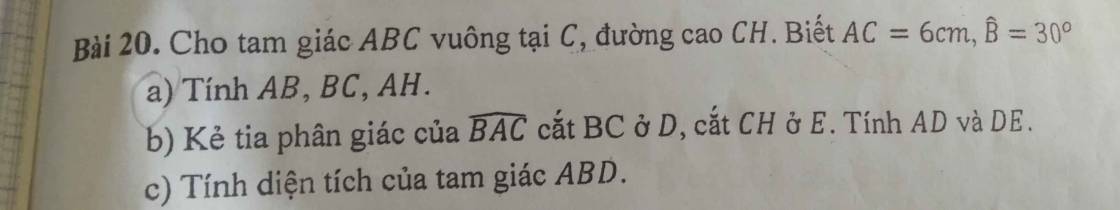a: Xét ΔCBA vuông tại C có
sin B=AC/BA
=>6/BA=sin30=1/2
=>BA=12(cm)
\(BC=\sqrt{12^2-6^2}=6\sqrt{3}\left(cm\right)\)
\(AH=\dfrac{AC^2}{AB}=\dfrac{36}{12}=3\left(cm\right)\)
b: góc CAD=1/2*góc BAC=60/2=30 độ
Xét ΔCAD vuông tại C có
cos DAC=CA/DA
=>6/DA=cos30
=>\(DA=4\sqrt{3}\left(cm\right)\)
c: Xét ΔDAB có góc DAB=góc DBA
nên ΔDAB cân tại D
=>góc BDA=180-2*góc DAB
=180-2*30=120 độ
\(S_{DAB}=\dfrac{1}{2}\cdot DA\cdot DB\cdot sinBDA=\dfrac{1}{2}\cdot4\sqrt{3}\cdot4\sqrt{3}\cdot sin120=12\sqrt{3}\left(cm^2\right)\)
Đúng 1
Bình luận (0)
