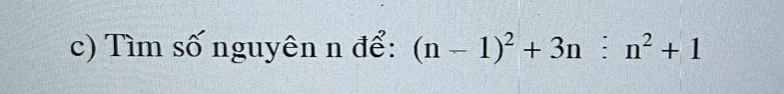Question

Answer 1

Ta có:

\(\left(n-1\right)^2+3n=n^2-2n+1+3n=\left(n^2+1\right)+\left(3n-2n\right)=\left(n^2+1\right)+n\)

Do \(n^2+1⋮n^2+1\) nên để \(\left(n-1\right)^2+3n⋮n^2+1\) thì \(n⋮n^2+1\)

\(\Rightarrow n^2⋮n^2+1\Rightarrow1⋮n^2+1\Leftrightarrow n=0\)

Answer 2

=>n chia hết cho n^2+1

=>n^2 chia hết cho n^2+1

=>n^2+1=1

=>n=0