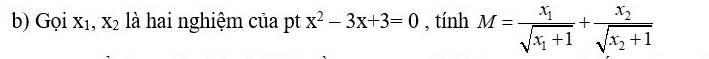\(M^2=\dfrac{x_1^2}{x_1+1}+\dfrac{x_2^2}{x_2+1}+\dfrac{x_1\cdot x_2}{\sqrt{x_1x_2+x_1+x_2+1}}\)
\(=\dfrac{x_1^2}{x_1+1}+\dfrac{x_2^2}{x_2+1}+\dfrac{3}{\sqrt{3+3+1}}\)
\(=\dfrac{x_1^2\cdot x_2+x_1^2+x_2^2\cdot x_1+x_2^2}{x_1x_2+x_1+x_2+1}+\dfrac{3}{\sqrt{7}}\)
\(=\dfrac{3}{\sqrt{7}}+\dfrac{3\cdot3+3^2-2\cdot3}{3+3+1}=\dfrac{3}{\sqrt{7}}+\dfrac{12}{7}=\dfrac{12+3\sqrt{7}}{7}\)
=>\(M=\sqrt{\dfrac{12+3\sqrt{7}}{7}}\)
Đúng 0
Bình luận (0)
