a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>BA=BE
c: Xét tứ giác ACBK có
M là trung điểm chung của AB và CK
=>ACBK là hình bình hành
=>AC=BK
AC+BC=BK+BC>CK=2CM
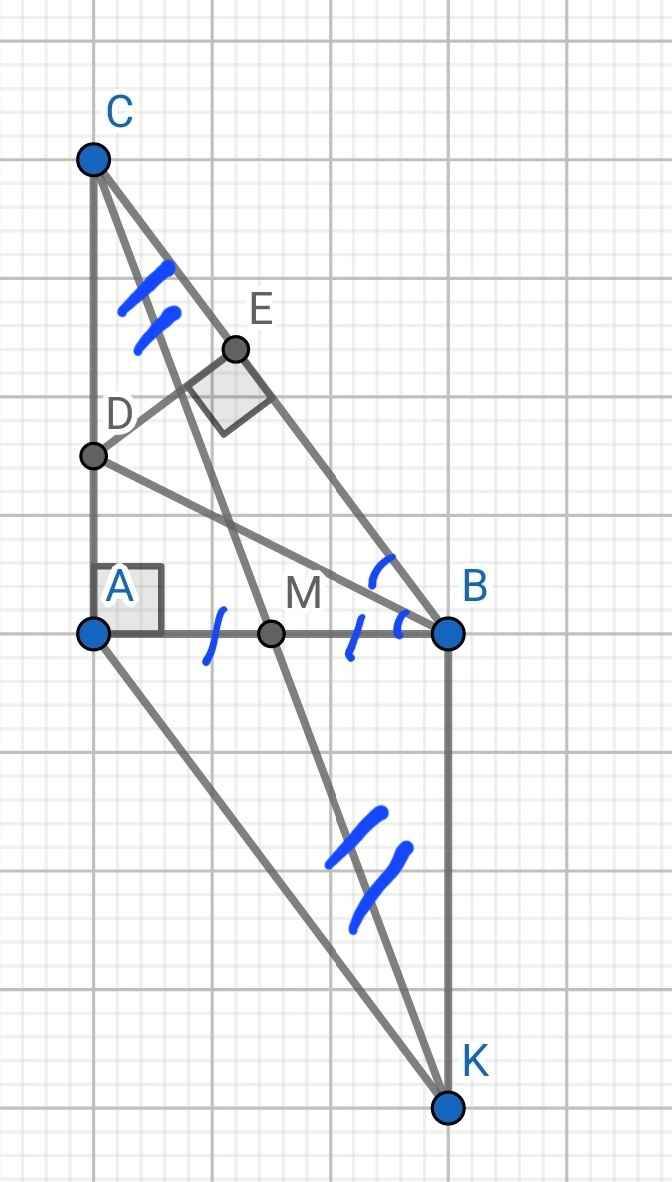
a) Xét hai tam giác vuông: ∆BAD và ∆BED có:
BD chung
∠ABD = ∠EBD (BD là phân giác ∠B)
⇒ ∆BAD = ∆BED (g-g)
b) Do ∆BAD = ∆BED (cmt)
⇒ BA = BE (hai cạnh tương ứng)
c) Xét ∆AMC và ∆BMK có:
AM = BM (M là trung điểm AB)
∠AMC = ∠BMK (đối đỉnh)
MC = MK (gt)
⇒ ∆AMC = ∆BMK (c-g-c)
⇒ AC = BK (hai cạnh tương ứng)
∆BCK có:
BC + BK > CK (bất đẳng thức tam giác)
Mà CK = 2CM
⇒ BC + BK > 2CM
Lại có AC = BK (cmt)
⇒ BC + AC > 2CM
Hay AC + BC > 2CM

















