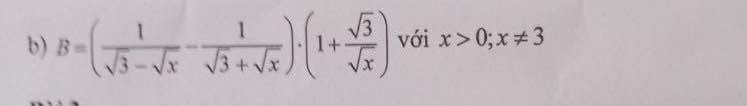Question

Answer 1

Với mọi \(x>0;x\ne3\), ta có : 

\(B=\left(\dfrac{1}{\sqrt{3}-\sqrt{x}}-\dfrac{1}{\sqrt{3}+\sqrt{x}}\right)\left(1+\dfrac{\sqrt{3}}{\sqrt{x}}\right)\)

\(=\dfrac{\sqrt{3}+\sqrt{x}-\sqrt{3}+\sqrt{x}}{\left(\sqrt{3}-\sqrt{x}\right)\left(\sqrt{3}+\sqrt{x}\right)}\cdot\dfrac{\sqrt{x}+\sqrt{3}}{\sqrt{x}}\)

\(=\dfrac{2\sqrt{x}}{\left(\sqrt{3}-\sqrt{x}\right)\left(\sqrt{3}+\sqrt{x}\right)}\cdot\dfrac{\sqrt{x}+\sqrt{3}}{\sqrt{x}}\)

\(=\dfrac{2}{\sqrt{3}-\sqrt{x}}\)

Vậy : Với mọi \(x>0;x\ne3\) thì \(B=\dfrac{2}{\sqrt{3}-\sqrt{x}}\)

Answer 2

.