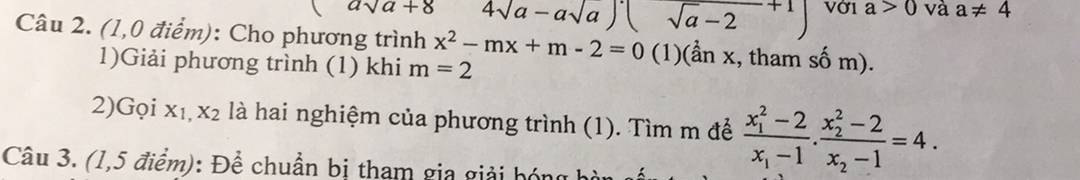1: Khi m=2 thì (1) sẽ là x^2-2x=0
=>x=0 hoặc x=2
2: Δ=(-m)^2-4(m-2)
=m^2-4m+8
=m^2-4m+4+4=(m-2)^2+4>0
=>(1) luôn có hai nghiệm phân biệt
\(\dfrac{x_1^2-2}{x_1-1}\cdot\dfrac{x_2^2-2}{x_2-1}=4\)
=>\(\dfrac{\left(x_1\cdot x_2\right)^2-2\left(x_1^2+x_2^2\right)+4}{x_1x_2-\left(x_1+x_2\right)+1}=4\)
=>\(\dfrac{\left(m-2\right)^2-2\left[\left(-m\right)^2-2\left(m-2\right)\right]+4}{\left(m-2\right)-\left(m\right)+1}=4\)
=>\(\dfrac{m^2-4m+4-2\left[m^2-2m+4\right]}{m-2-m+1}=4\)
=>\(m^2-4m+4-2m^2+8m-16=4\cdot\left(-1\right)=-4\)
=>\(-m^2+4m-12+4=0\)
=>-m^2+4m-8=0
=>m^2-4m+8=0
=>(m-2)^2+4=0(loại)
Đúng 1
Bình luận (0)
