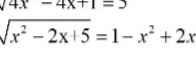`\sqrt{x^2-2x+5}=1-x^2+2x` `ĐK:1-\sqrt{2} <= x <= 1+\sqrt{2}`
`<=>\sqrt{x^2-2x+5}=-(x^2-2x+5-6)`
Đặt `\sqrt{x^2-2x+5}=t` `(t >= 0)` khi đó ta có:
`t=-(t^2-6)`
`<=>t^2+t-6=0`
`<=>[(t=2 (t//m)),(t=-3(ko t//m)):}`
`=>t=2=>\sqrt{x^2-2x+5}=2`
`<=>x^2-2x+5=4`
`<=>x^2-2x+1=0`
`<=>(x-1)^2=0<=>x=1` (t/m)
Vậy `S={1}`
\(\Leftrightarrow\sqrt{x^2-2x+5}=-\left(x^2-2x-1\right)=-\left(x^2-2x+5-6\right)\)
Đặt x^2-2x+5=a
Pt trở thành \(\sqrt{a}=-a+6\)
=>\(\left\{{}\begin{matrix}a< =6\\a^2=-a+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a< =6\\\left(a+3\right)\left(a-2\right)=0\end{matrix}\right.\Leftrightarrow a\in\left\{-3;2\right\}\)
Khi a=-3 thì \(x^2-2x+5=-3\)(loại)
Khi a=2 thì \(x^2-2x+5=2\)
=>x^2-2x+3=0(loại)