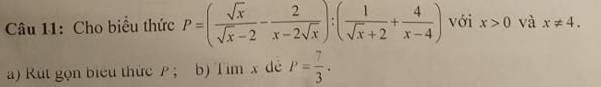`(a):P=((\sqrt{x})/(\sqrt{x}-2)-(2)/(x-2\sqrt{x})):((1)/(\sqrt{x}+2)+(4)/(x-4))` `(x>0;x\ne 4)`
`=((\sqrt{x})/(\sqrt{x}-2)-(2)/(\sqrt{x}(\sqrt{x}-2))):((1)/(\sqrt{x}+2)+(4)/((\sqrt{x}-2)(\sqrt{x}+2)))`
`=(x-2)/(\sqrt{x}(\sqrt{x}-2)):(\sqrt{x}-2+4)/((\sqrt{x}-2)(\sqrt{x}+2))`
`=(x-2)/(\sqrt{x}(\sqrt{x}-2)).((\sqrt{x}-2)(\sqrt{x}+2))/(\sqrt{x}+2)`
`=(x-2)/(\sqrt{x})`
`(b):P=7/3<=>(x-2)/(\sqrt{x})=7/3`
`<=>3(x-2)=7\sqrt{x}`
`<=>3x-6-7\sqrt{x}=0`
`<=>(3x-9\sqrt{x})+(2\sqrt{x}-6)=0`
`<=>3\sqrt{x}(\sqrt{x}-3)+2(\sqrt{x}-3)=0`
`<=>(\sqrt{x}-3)(3\sqrt{x}+2)=0`
`=>\sqrt{x}-3=0` ( Do : `3\sqrt{x}+2>0` với mọi `x\in ĐK ` )
`<=>x=9\ (TMDK)`
\(a,P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{2}{\sqrt{x}\left(\sqrt{x}-2\right)}\right):\left(\dfrac{\sqrt{x}-2+4}{x-4}\right)\\ =\left(\dfrac{x-2}{\sqrt{x}\left(\sqrt{x}-2\right)}\right).\dfrac{x-4}{\sqrt{x}+2}\\ =\dfrac{\sqrt{x}-2}{\sqrt{x}}\\ b,P=\dfrac{7}{3}\\ \dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{7}{3}\\ 3\sqrt{x}-6=7\sqrt{x}\\ 3\sqrt{x}-7\sqrt{x}=6\\-4\sqrt{x}=6\\ \sqrt{x}=-\dfrac{6}{4}\left(voli\right)\\ =>\varnothing\)
Vậy ko có giá trị nào của x để \(P=7/3\)