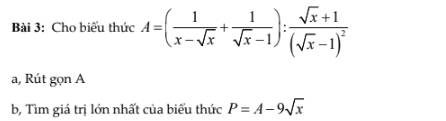a: \(=\dfrac{1+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{1+\sqrt{x}}=\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
b: \(P=A-9\sqrt{x}=\dfrac{\sqrt{x}-1-9x}{\sqrt{x}}\)
\(=\dfrac{-9\left(x-\dfrac{1}{9}\sqrt{x}+\dfrac{1}{9}\right)}{\sqrt{x}}\)
\(=\dfrac{-9\left(x-\dfrac{1}{9}\sqrt{x}+\dfrac{1}{324}+\dfrac{35}{324}\right)}{\sqrt{x}}\)
\(=\dfrac{-9\left(\sqrt{x}-\dfrac{1}{18}\right)^2-\dfrac{35}{36}}{\sqrt{x}}< =-\dfrac{35}{36}\)
Dấu = xảy ra khi x=1/324
Đúng 0
Bình luận (0)
