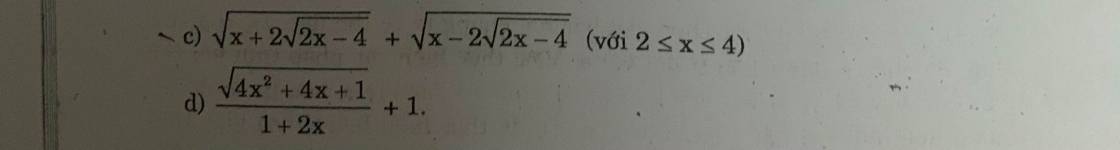c, \(A^2=x+2\sqrt{2x-4}+x-2\sqrt{2x-4}+2\sqrt{x^2-4\left(2x-4\right)}\)
\(=2x+2\sqrt{x^2-8x+16}=2x+2\left|x-4\right|=2x-2\left(x-4\right)=8\)
\(\Rightarrow A=2\sqrt{2}\)
d, \(\dfrac{\sqrt{\left(2x+1\right)^2}}{2x+1}+1=\dfrac{\left|2x+1\right|}{2x+1}+1\)
Với x > -1/2 thì d, = 1 + 1 = 2
Với x < -1/2 thì d, - 1 + 1 = 0
d: \(=\sqrt{x-2+2\sqrt{x-2}\cdot\sqrt{2}+2}+\sqrt{x-2-2\sqrt{x-2}\cdot\sqrt{2}+2}\)
\(=\left|\sqrt{x-2}+\sqrt{2}\right|+\left|\sqrt{x-2}-\sqrt{2}\right|\)
\(=\sqrt{x-2}+\sqrt{2}+\sqrt{2}-\sqrt{x-2}=2\sqrt{2}\)
d: \(=\dfrac{\left|2x+1\right|}{2x+1}+1=1+1=2\)