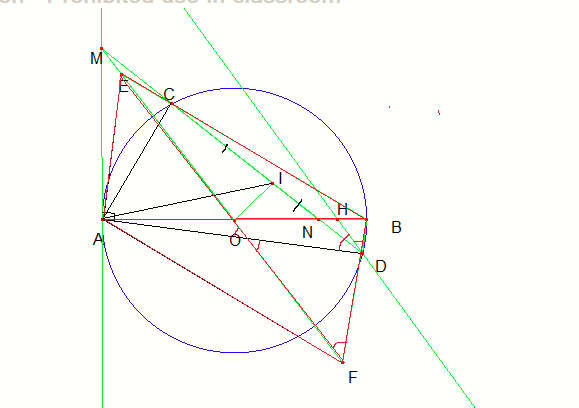
a> Vì I là trung điểm của CD <gt>
=> OI \(\perp\)CD
=> MIO = 90 độ
Ta có AM là tiếp tuyến của đường tròn tâm O
=> MAO = 90 độ
Xét tứ giác AMIO có :
MAO+MIO=180
Mà 2 góc này ở vị trí đối diện nhau
=> Tứ giác AMIO nội tiếp <đpcm>
b>
Xét đường tròn tâm O ta có :
MAC = MDA = \(\dfrac{1}{2}\)sđ cung AC
Xét tam giác MAC và tam giác MDA có:
MAC=MDA
DMA chung
=> \(\Delta MAC\sim\Delta MDA\left(g-g\right)\)
=> \(\dfrac{MA}{MD}=\dfrac{MC}{MA}\)
=>\(MA^2=MC.MD\) <đpcm>
Vì đường thẳng qua D // với MO <gt>
=> MDH = DMO <2 góc so le trong> *
Vì tứ giác AMIO nội tiếp <cma>
=> DMO=IAO cùng chắn cung OI **
Từ * và ** => MDH=IAO <đpcm>














