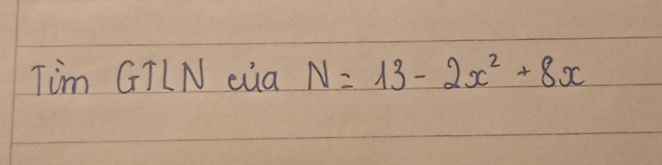\(N=-2\left(x^2-4x-\dfrac{13}{2}\right)\)
\(=-2\left(x^2-4x+4-\dfrac{21}{2}\right)\)
\(=-2\left(x-2\right)^2+21\le21\)
Dấu '=' xảy ra khi x=2
`N=13-2x^2+8x`
`N=-2(x^2-4x-13/2)`
`N=-2(x^2-4x+4-21/2)`
`N=-2(x-2)^2+21`
Vì `-2(x-2)^2 <= 0 AA x`
`<=>-2(x-2)^2+21 <= 21 AA x`
Hay `N <= 21 AA x`
Dấu "`=`" xảy ra `<=>(x-2)^2=0<=>x=2`
Vậy `GTN N` của `N` là `21` khi `x=2`
N = -2.(x² - 4x - \(\dfrac{13}{2}\))
= -2.[x² - 4x + 4 +(\(\dfrac{5}{2}\))]
= -2.[ (x² - 2.2.x + 2²) + (\(\dfrac{5}{2}\))]
= -2.[ (x -2)² + (\(\dfrac{5}{2}\))]
Có: (x -2)² ≥ 0 với mọi x
(x - 2)² + (\(\dfrac{5}{2}\)) ≥ \(\dfrac{5}{2}\)
-2. [(x - 2)² + \(\dfrac{5}{2}\))] ≤ -5
Vậy GTLN là -5 khi x - 2 = 0 -> x = 2