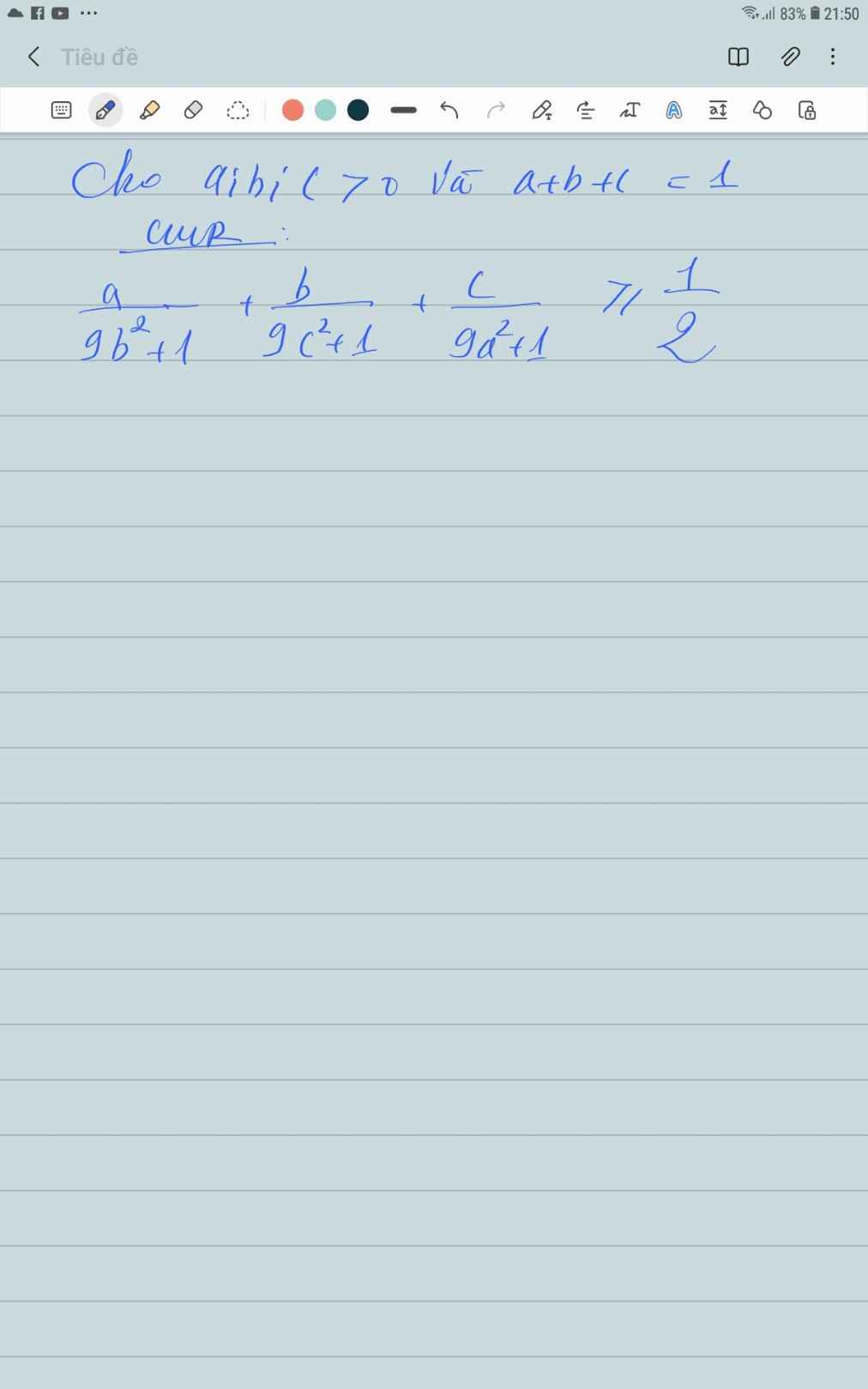có \(\dfrac{a}{9b^2+1}=a-\dfrac{9ab^2}{9b^2+1},\dfrac{b}{9c^2+1}=b-\dfrac{9bc^2}{9c^2+1},\dfrac{c}{9a^2+1}=c-\dfrac{9ca^2}{9a^2+1}\)
<=> P = \(a-\dfrac{9ab^2}{9b^2+1}+b-\dfrac{9bc^2}{9c^2+1}+c-\dfrac{9ca^2}{9a^2+1}\ge a+b+c-\dfrac{9ab^2}{2\sqrt{9b^2}}-\dfrac{9bc^2}{2\sqrt{9c^2}}-\dfrac{9ca^2}{2\sqrt{9a^2}}=1-\dfrac{3}{2}\left(ab+bc+ac\right)\ge1-\dfrac{3}{2}.\left(a+b+c\right)^2.\dfrac{1}{3}=1-\dfrac{1}{2}=\dfrac{1}{2}\)
Dấu bằng xảy ra khi a=b=c=1/3
Đúng 2
Bình luận (0)
