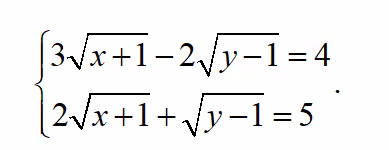\(\Leftrightarrow\left\{{}\begin{matrix}3\sqrt{x+1}-2\sqrt{y-1}=4\\4\sqrt{x+1}+2\sqrt{y-1}=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7\sqrt{x+1}=14\\2\sqrt{x+1}+\sqrt{y-1}=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x+1}=2\\\sqrt{y-1}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\end{matrix}\right.\)
\(ĐK:x\ge-1;y\ge1\)
Đặt \(\sqrt{x+1}=a;a\ge0\)
\(\sqrt{y-1}=b;b\ge0\)
hpt trở thành:
\(\left\{{}\begin{matrix}3a-2b=4\\2a+b=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x+1}=2\\\sqrt{y-1}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+1=4\\y-1=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\end{matrix}\right.\) ( tm )
Vậy nghiệm hpt (x;y) = (3;2)
Không cần đặt ẩn phụ mà ng/ta vẫn giải được.