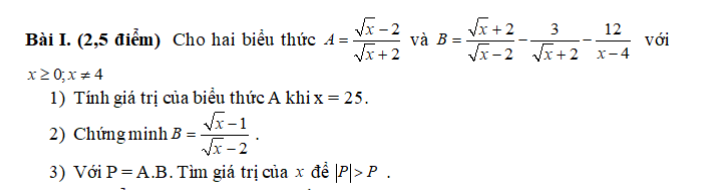1: Thay x=25 vào A, ta được:
\(A=\dfrac{5-2}{5+2}=\dfrac{3}{7}\)
2: \(B=\dfrac{x+4\sqrt{x}+4-3\sqrt{x}+6-12}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
1, Thay x = 25 ta được
\(A=\dfrac{5-2}{5+2}=\dfrac{3}{7}\)
2, Với x >= 0 ; x khác 4
\(B=\dfrac{x+4\sqrt{x}+4-3\sqrt{x}+6-12}{x-4}=\dfrac{x+\sqrt{x}-2}{x-4}=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)(đpcm)
3, Ta có \(P=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)
Lại có \(\left|P\right|>P\Rightarrow0>\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\Rightarrow\sqrt{x}-1>0\Leftrightarrow x>1\)
Kết hợp đk vậy x > 1 ; x khác 4
mình sửa câu 3 do nãy cập nhật rồi mà nó ko có lên hình :'(( sôù
Ta có : \(P=AB=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)
Để \(\left|P\right|>P\Rightarrow P< 0\Leftrightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+2}< 0\Rightarrow\sqrt{x}-1< 0\Leftrightarrow x< 1\)
Kết hợp đk vậy 0 =< x < 1