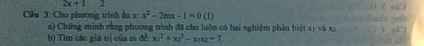Câu 3:
a) Ta có: \(x^2-2mx-1=0\)
\(\Delta=b^2-4ac=4m^2+4\ge4>0\forall m\)
Vậy phương trình đã cho luôn có hai nghiệm phân biệt \(x_1\) và \(x_2\).
b) \(x^2_1+x^2_2-x_1x_2=7\) (1)
Theo hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-1\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left(x^2_1+2x_1x_2+x^2_2\right)-2x_1x_2-x_1x_2=7\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2=7\)
\(\Rightarrow\left(2m\right)^2-3.\left(-1\right)=7\)
\(\Leftrightarrow4m^2-4=0\)
\(\Leftrightarrow m=\pm1\)
Vậy \(m=\pm1\) thì \(x^2_1+x^2_2-x_1x_2=7\).
a: \(\Delta=\left(-2m\right)^2-4\cdot1\cdot\left(-1\right)=4m^2+4>0\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
b: Theo đề, ta có: \(\left(x_1+x_2\right)^2-3x_1x_2=7\)
\(\Leftrightarrow4m^2-3\cdot\left(-1\right)=7\)
\(\Leftrightarrow m\in\left\{1;-1\right\}\)