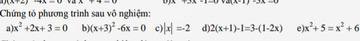\(a,x^2+2x+3=0\\ \Leftrightarrow\left(x^2+2x+1\right)+2=0\\ \Leftrightarrow\left(x+1\right)^2+2=0\)
Vì \(\left(x+1\right)^2\ge0\forall x,2>0\Rightarrow\left(x+1\right)^2+2>0\)
Vậy pt vô nghiệm
\(b,\left(x+3\right)^2-6x=0\\ \Leftrightarrow x^2+6x+9-6x=0\\ \Leftrightarrow x^2+9=0\)
Vì \(x^2\ge0\forall x,9>0\Rightarrow x^2+9>0\)
Vậy pt vô nghiệm
\(c,\left|x\right|=-2\)
Vì \(\left|x\right|\ge0\forall x\) mà -2 <0
Vậy pt vô nghiệm
\(d,2\left(1+x\right)-1=3-\left(1-2x\right)\\ \Leftrightarrow2+2x-1=3-1+2x\\ \Leftrightarrow2x+1=2x+2\\ \Leftrightarrow2x+2-2x-1=0\\ \Leftrightarrow0x-1=0\\ \Leftrightarrow0x=1\left(vô.lí\right)\)
Vậy pt vô nghiệm
\(e,x^2+5=x^2+6\\ \Leftrightarrow x^2+6-x^2-5=0\\ \Leftrightarrow0x-1=0\Leftrightarrow0x=1\left(vô.lí\right)\)
Vậy pt vô nghiệm
a: \(\text{Δ}=2^2-4\cdot1\cdot3=4-12=-8< 0\)
=>Phương trình vô nghiệm
b: \(\Leftrightarrow x^2+6x+9-6x=0\)
\(\Leftrightarrow x^2+9=0\)(vô lý)
=>Ptvn
c: \(\left|x\right|=-2\)
mà |x|>=0 với mọi x
nên \(x\in\varnothing\)
d: \(\Leftrightarrow2x+2-1=3-1+2x\)
=>2=3(vô lý)
e: \(\Leftrightarrow5=6\)(vô lý)
a)\(x^2+2x+3=0\)
\(x^2+2x+1+2=0\)
\(\left(x+1\right)^2+2=0\)
có \(\left(x+1\right)^2\ge0\) ; 2 > 0
\(\Rightarrow\left(x+1\right)^2+2\ne0\) hay \(x^2+2x+3\ne0\) ( vô nghiệm)
b) \(\left(x+3\right)^2-6x=0\)
\(x^2+6x+9-6x=0\)
\(x^2+9=0\)
\(x^2=-9\) ( vô lí) \(\Rightarrow\left(x+3\right)^2-6x\ne0\) ( vô nghiệm)
c)\(\left|x\right|=-2\)
Ta có: |x| > 0 với mọi x
mà -2<0
\(\left|x\right|=-2\)
=> phương trình vô nghiệm
d)\(x^2+5=x^2+6\)
\(x^2-x^2=6-5\)
\(0=1\) ( vô lí )
=> phương trình vô nghiệm
a: Δ=22−4⋅1⋅3=4−12=−8<0Δ=22−4⋅1⋅3=4−12=−8<0
=>Phương trình vô nghiệm
b: ⇔x2+6x+9−6x=0⇔x2+6x+9−6x=0
⇔x2+9=0⇔x2+9=0(vô lý)
=>Ptvn
c: |x|=−2|x|=−2
mà |x|>=0 với mọi x
nên x∈∅x∈∅
d: ⇔2x+2−1=3−1+2x⇔2x+2−1=3−1+2x
=>2=3(vô lý)
e: ⇔5=6⇔5=6(vô lý)