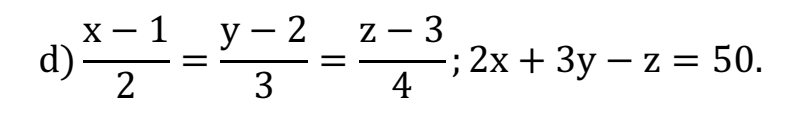Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}=\dfrac{2x+3y-z-2-6+3}{2\cdot2+3\cdot3-4}=\dfrac{45}{9}=5\)
Do đó: x-1=10; y-2=15; z-3=20
=>x=11; y=17; z=23
\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}\text{ và }2x+3y-z=50\)
\(\text{Áp dụng tính chất dãy tỉ số bằng nhau:}\)
\(\dfrac{2x-2+3y-6-z+3}{4+9-4}=\dfrac{\left(2x+3y-z\right)-\left(2+6-3\right)}{9}=\dfrac{50-5}{9}=5\)
\(\Rightarrow\dfrac{2x-2}{4}=5\Rightarrow2x-2=20\Rightarrow2x=22\Rightarrow x=11\)
\(\dfrac{3y-6}{9}=5\Rightarrow3y-6=45\Rightarrow3y=51\Rightarrow y=17\)
\(\dfrac{z-3}{4}=5\Rightarrow z-3=20\Rightarrow z=23\)