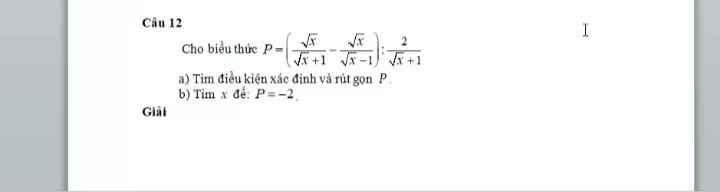a, ĐKXĐ:\(\left\{{}\begin{matrix}\sqrt{x}+1\ne0\left(luôn.đúng\right)\\\sqrt{x}-1\ne0\end{matrix}\right.\Rightarrow\sqrt{x}\ne1\Rightarrow x\ne1\)
\(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{\sqrt{x}}{\sqrt{x}-1}\right):\dfrac{2}{\sqrt{x}+1}\)
\(\Rightarrow P=\left(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right).\dfrac{\sqrt{x}+1}{2}\)
\(\Rightarrow P=\left(\dfrac{x-\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{x+\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right).\dfrac{\sqrt{x}+1}{2}\)
\(\Rightarrow P=\dfrac{x-\sqrt{x}-x-\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\dfrac{\sqrt{x}+1}{2}\)
\(\Rightarrow P=\dfrac{-2\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\dfrac{\sqrt{x}+1}{2}\)
\(\Rightarrow P=\dfrac{-\sqrt{x}}{\sqrt{x}-1}\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{1-\sqrt{x}}\)
b, \(\dfrac{\sqrt{x}}{1-\sqrt{x}}=-2\)
\(\Rightarrow\sqrt{x}=-2\left(1-\sqrt{x}\right)\)
\(\Rightarrow\sqrt{x}=2\sqrt{x}-2\)
\(\Rightarrow\sqrt{x}-2=0\)
\(\Rightarrow\sqrt{x}=2\)
\(\Rightarrow x=4\left(tm\right)\)