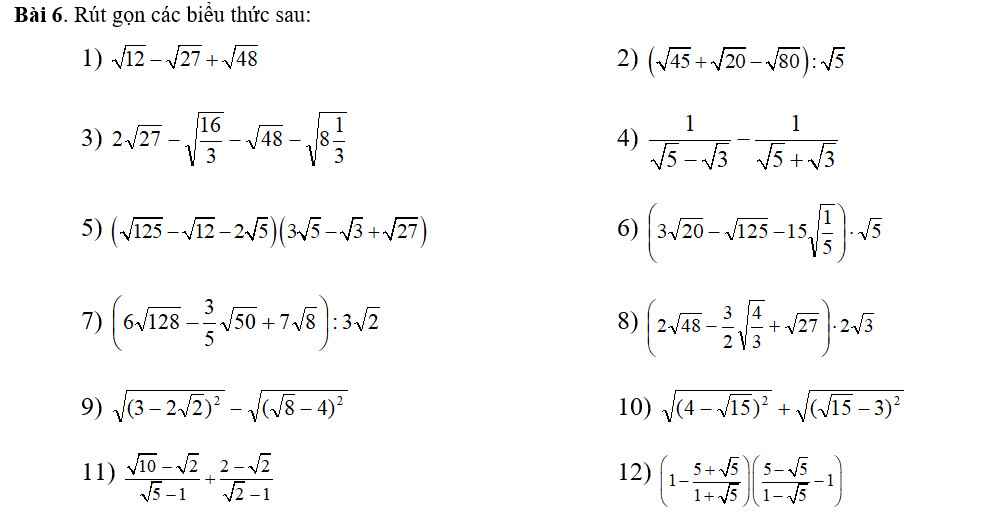1: \(=2\sqrt{3}-3\sqrt{3}+4\sqrt{3}=3\sqrt{3}\)
2: =3+2-4
=1
\(1,=2\sqrt{3}-3\sqrt{3}+4\sqrt{3}=3\sqrt{3}\\ 2,=\left(3\sqrt{5}+2\sqrt{5}-4\sqrt{5}\right):\sqrt{5}=\sqrt{5}:\sqrt{5}=1\\ 3,=6\sqrt{3}-\dfrac{4\sqrt{3}}{3}-4\sqrt{3}-\dfrac{5\sqrt{3}}{3}=2\sqrt{3}-\dfrac{9\sqrt{3}}{3}=2\sqrt{3}-3\sqrt{3}=-\sqrt{3}\\ 4,=\dfrac{\sqrt{5}+\sqrt{3}-\sqrt{5}+\sqrt{3}}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\\ 5,=\left(5\sqrt{5}-2\sqrt{3}-2\sqrt{5}\right)\left(3\sqrt{5}-\sqrt{3}+3\sqrt{3}\right)\\ =\left(3\sqrt{5}-2\sqrt{3}\right)\left(3\sqrt{5}+2\sqrt{3}\right)=45-12=33\)
\(6,=\left(6\sqrt{5}-5\sqrt{5}-3\sqrt{5}\right)\cdot\sqrt{5}=-2\sqrt{5}\cdot\sqrt{5}=-10\\ 7,=\left(48\sqrt{2}-3\sqrt{2}+14\sqrt{2}\right):3\sqrt{2}=59\sqrt{2}:3\sqrt{2}=\dfrac{59}{3}\\ 8,=\left(8\sqrt{3}-\sqrt{3}+3\sqrt{3}\right)\cdot2\sqrt{3}=10\sqrt{3}\cdot2\sqrt{3}=60\\ 9,=3-2\sqrt{2}-4+2\sqrt{2}=-1\\ 10,=4-\sqrt{15}+\sqrt{15}-3=1\\ 11,=\dfrac{\sqrt{2}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{2}+\sqrt{2}=2\sqrt{2}\\ 12,=\left(1-\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}\right)\left(\dfrac{\sqrt{5}\left(\sqrt{5}-1\right)}{1-\sqrt{5}}-1\right)\\ =\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)=5-1=4\)