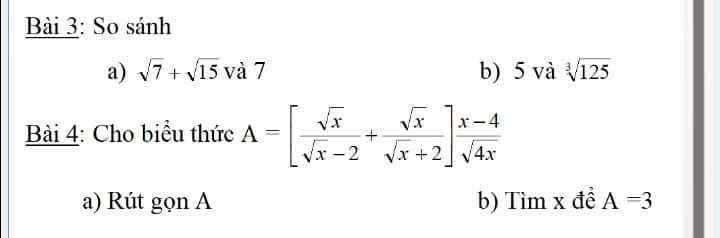Question

Answer 1

Bài 4:

)\(\left[\dfrac{\sqrt{x}}{\sqrt{x}-2}+\dfrac{\sqrt{x}}{\sqrt{x}+2}\right]\dfrac{x-4}{\sqrt{4x}}\\ DKXD:x>4;x\ne0\\ =\left[\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)+\sqrt{x}\left(\sqrt{x}-2\right)}{x-4}\right]\dfrac{x-4}{2\sqrt{x}}\\ =\left[\dfrac{x+2\sqrt{x}+x-2\sqrt{x}}{x-4}\right]\dfrac{x-4}{2\sqrt{x}}\\ =\dfrac{2x}{x-4}.\dfrac{x-4}{2\sqrt{x}}=\sqrt{x}\\ b.A=3\\ \Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tmdk\right)\)

Vậy x=9 thì A=3

Answer 2

Bài 3: 

b: \(5=\sqrt[3]{125}\)