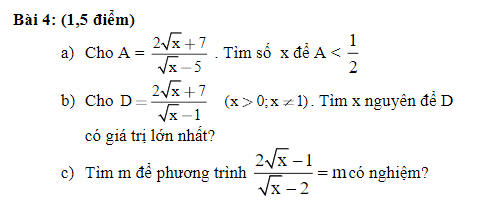a: Để \(A< \dfrac{1}{2}\) thì \(\dfrac{4\sqrt{x}+14-\sqrt{x}+5}{2\left(\sqrt{x}-5\right)}< 0\)
\(\Leftrightarrow0\le x< 25\)
\(a,A< \dfrac{1}{2}\Leftrightarrow\dfrac{2\sqrt{x}+7}{\sqrt{x}-5}-\dfrac{1}{2}< 0\\ \Leftrightarrow\dfrac{4\sqrt{x}+14-\sqrt{x}+5}{2\left(\sqrt{x}-5\right)}=\dfrac{3\sqrt{x}+19}{2\left(\sqrt{x}-5\right)}< 0\\ \Leftrightarrow\sqrt{x}-5< 0\Leftrightarrow x< 25\\ \Leftrightarrow0\le x< 25\)
\(b,D=\dfrac{2\sqrt{x}+7}{\sqrt{x}-1}=2+\dfrac{9}{\sqrt{x}-1}\)
Vì \(\dfrac{9}{\sqrt{x}-1}\le\dfrac{9}{1}=9\Leftrightarrow D\le2+9=11\)
\(D_{max}=11\Leftrightarrow x=0\)