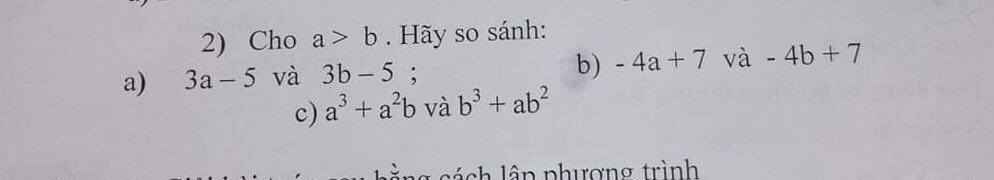Question

Answer 1

a: ta có: a>b

nên 3a>3b

hay 3a-5>3b-5

b: ta có: a>b

nên -4a<-4b

hay -4a+7<-4b+7

c: Ta có: \(a^3+a^2b=a^2\left(a+b\right)\)

\(b^3+ab^2=b^2\left(a+b\right)\)

mà \(a^2>b^2\)

nên \(a^3+a^2b>b^3+ab^2\)

Answer 2

 a/ Ta có: \(a>b\Rightarrow3a>3b\Rightarrow3a-5>3b-5\)

Vậy: \(3a-5>3b-5\)

==========

b/ Ta có: \(a>b\Rightarrow4a>4b\Rightarrow-4a< -4b\Rightarrow-4a+7< -4b+7\)

Vậy: \(-4a+7< -4b+7\)