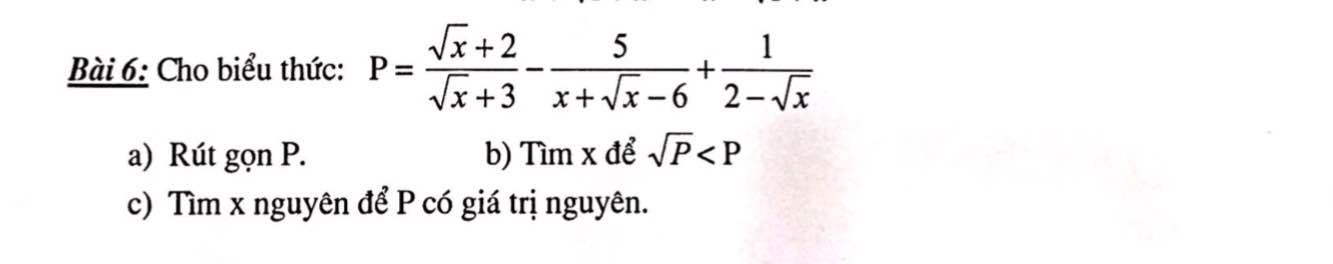\(a,P=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{5}{x+\sqrt{x}-6}+\dfrac{1}{2-\sqrt{x}}\left(x\ge0;x\ne4\right)\\ P=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)-5-\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ P=\dfrac{x-4-5-\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ P=\dfrac{x-\sqrt{x}-12}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ P=\dfrac{\left(\sqrt{x}-4\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)
\(b,\)Để \(\sqrt{P}< P\Leftrightarrow\sqrt{P}\left(1-\sqrt{P}\right)< 0\Leftrightarrow1-\sqrt{P}< 0\left(\sqrt{P}\ge0\right)\)
\(\Leftrightarrow\sqrt{P}>1\Leftrightarrow P>1\Leftrightarrow P-1>0\\ \Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}-1>0\\ \Leftrightarrow\dfrac{\sqrt{x}-4-\sqrt{x}+2}{\sqrt{x}-2}>0\\ \Leftrightarrow\dfrac{-2}{\sqrt{x}-2}>0\Leftrightarrow\sqrt{x}-2< 0\left(-2 < 0\right)\\ \Leftrightarrow\sqrt{x}< 2\Leftrightarrow x< 4\)
\(c,P=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}=\dfrac{\sqrt{x}-2-2}{\sqrt{x}-2}=1-\dfrac{2}{\sqrt{x}-2}\)
Để \(P\in Z\Leftrightarrow2⋮\left(\sqrt{x}-2\right)\)
\(\Leftrightarrow\sqrt{x}-2\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{0;1;3;4\right\}\\ \Leftrightarrow x\in\left\{0;1;9;16\right\}\)
a: Ta có: \(P=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{5}{x+\sqrt{x}-6}+\dfrac{1}{2-\sqrt{x}}\)
\(=\dfrac{x-4-5-\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)
c: Để P nguyên thì \(-2⋮\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}-2\in\left\{1;-1;2;-2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{3;1;4;0\right\}\)
hay \(x\in\left\{9;1;16;0\right\}\)