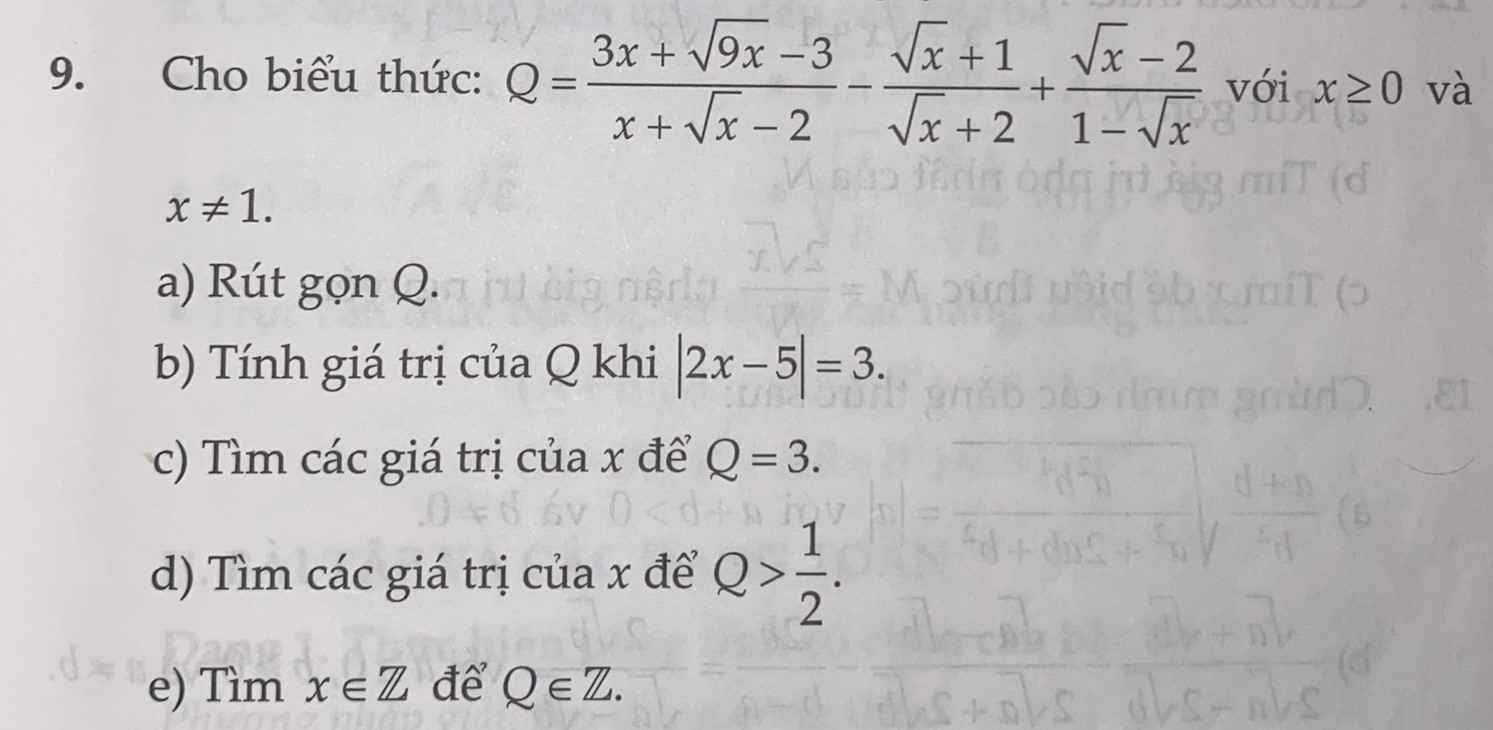a. \(Q=\dfrac{3x+\sqrt{9x}-3}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{\sqrt{x}-2}{1-\sqrt{x}}\)
\(=\dfrac{3x+3\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}-\dfrac{x-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}-\dfrac{x-4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{x+3\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b. Ta có \(\left|2x-5\right|=3\) \(\Leftrightarrow\left[{}\begin{matrix}2x-5=3\\5-2x=3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=1\end{matrix}\right.\) \(\Leftrightarrow x=4\)
Thay \(x=4\) vào \(Q\), ta được
\(Q=\dfrac{\sqrt{4}+1}{\sqrt{4}-1}=\dfrac{2+1}{2-1}=3\)
c. Ta có \(Q=3\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=3\Leftrightarrow\sqrt{x}+1=3\left(\sqrt{x}-1\right)\Leftrightarrow\sqrt{x}+1=3\sqrt{x}-3\Leftrightarrow4\sqrt{x}=4\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\)
d. Ta có \(Q>\dfrac{1}{2}\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-1}>\dfrac{1}{2}\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{1}{2}>0\Leftrightarrow\dfrac{\sqrt{x}+3}{2\left(\sqrt{x}-1\right)}>0\)
mà \(x\ge0\Leftrightarrow\sqrt{x}\ge0\Leftrightarrow\sqrt{x}+3\ge3>0\), nên để \(\dfrac{\sqrt{x}+3}{2\left(\sqrt{x}-1\right)}>0\) thì \(2\left(\sqrt{x}-1\right)>0\Leftrightarrow\sqrt{x}-1>0\Leftrightarrow\sqrt{x}>1\Leftrightarrow x>1\)
e. \(Q=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=1+\dfrac{2}{\sqrt{x}-1}\)
Để \(Q\) nhận giá trị nguyên thì \(\left(\sqrt{x}-1\right)\inƯ\left(2\right)=\left\{1;-1;2;-2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}-1=1\\\sqrt{x}-1=-1\\\sqrt{x}-1=2\\\sqrt{x}-1=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=2\\\sqrt{x}=0\\\sqrt{x}=3\\\sqrt{x}=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=4\\x=0\\x=9\end{matrix}\right.\)
Vậy tất cả các x thỏa ycbt là x=4; x=0 hoặc x=9
a: Ta có: \(Q=\dfrac{3x+3\sqrt{x}-3}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{\sqrt{x}-2}{1-\sqrt{x}}\)
\(=\dfrac{3x+3\sqrt{x}-3-x+1-x+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+3\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b: Ta có: |2x-5|=3
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=3\\2x-5=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=8\\2x=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(nhận\right)\\x=1\left(loại\right)\end{matrix}\right.\)
Thay x=4 vào Q, ta được:
\(Q=\dfrac{2+1}{2-1}=3\)