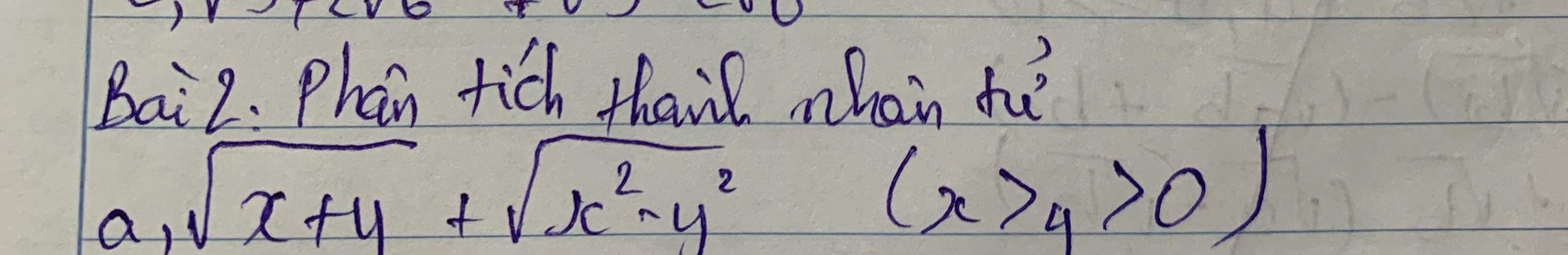Question

Answer 1

\(\sqrt{x+y}+\sqrt{x^2-y^2}\\ =\sqrt{x+y}+\sqrt{\left(x+y\right)\left(x-y\right)}\\ =\sqrt{x+y}+\sqrt{x+y}.\sqrt{x-y}\\ =\sqrt{x+y}\left(1+\sqrt{x-y}\right)\)

Answer 2

\(\sqrt{x+y}+\sqrt{x^2-y^2}\)

\(=\sqrt{x+y}\left(1+\sqrt{x-y}\right)\)

Answer 3

\(\sqrt{x+y}+\sqrt{x^2-y^2}=\sqrt{x+y}+\sqrt{\left(x+y\right)\left(x-y\right)}=\sqrt{x+y}\left(1+\sqrt{x-y}\right)\)